Các mạng nơ-ron truyền thẳng nhiều lớp nhiều lớp (multilayer perceptron) chỉ được xây dựng để nhận dữ liệu đầu vào dưới dạng vector. Đối với một số loại dữ liệu, đặc biệt là dữ liệu ở dạng hình ảnh, mạng nơ-ron truyền thẳng nhiều lớp tỏ ra không hiệu quả để đáp ứng xử lý tốt. Để áp dụng mạng nơ-ron truyền thẳng nhiều lớp cho việc xử lý các dữ liệu ở dạng hình ảnh, chúng ta cần phải chuyển đổi được hình ảnh về dưới dạng vector. Điều này thường gây ra sự mất mát nhiều thông tin trong dữ liệu gốc ban đầu. Mạng nơ-ron tích chập (Convolutional Neural Networks - CNN) được giới thiệu bởi LeCun đã lược bỏ công việc trích xuất các đặc trưng một cách thủ công. Mạng CNN là một kiến trúc mạng nơ-ron học sâu đặc biệt được thiết kế để xử lý dữ liệu hình ảnh và video, có khả năng học và trích xuất đặc trưng từ ảnh.

Mạng CNN được có kiến trúc được cấu tạo bởi một số loại layer bao gồm:

• Convolutional layer
• Pooling layer
• Fully connected layer

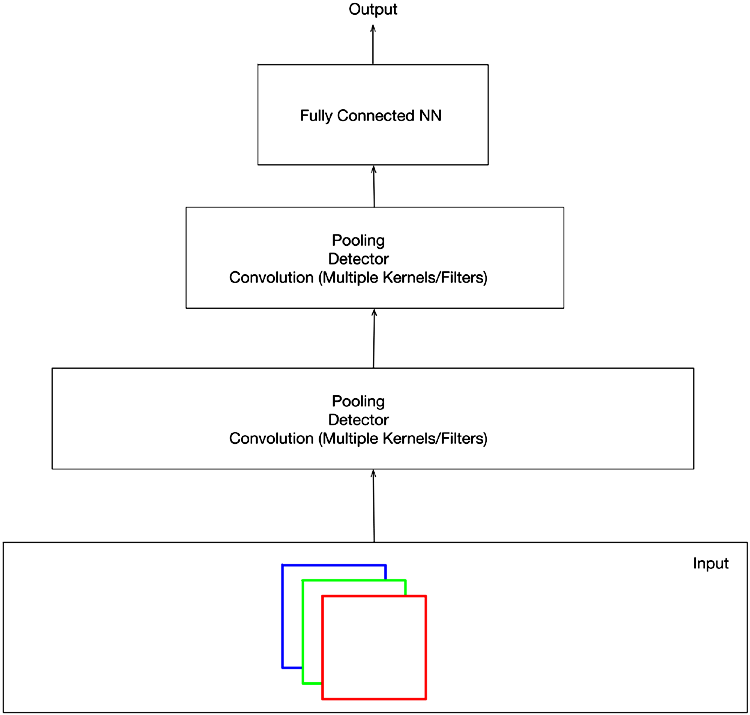
Convolutional layer thực hiện phép tích chập giữa ảnh đầu vào và các bộ lọc để tìm ra các đặc trưng của hình ảnh. Tiếp sau đó pooling layer làm giảm kích thước của đầu ra của convolutional layer để giảm độ phức tạp tính toán và ngăn chặn overfitting. Cuối cùng fully connected layer kết hợp các đặc trưng đã được trích xuất bởi convolutional layer và pooling layer để phân loại hình ảnh hoặc thực hiện các nhiệm vụ liên quan đến xử lý hình ảnh và video.

Mạng CNN là một loại mạng nơ-ron học sâu được sử dụng rộng rãi trong các ứng dụng liên quan đến xử lý hình ảnh và video, bao gồm nhận dạng hình ảnh, phân loại hình ảnh, xử lý video và nhận dạng khuôn mặt.

Phép tích chập (convolution operation)

Để đào sâu và hiểu rõ hơn về mạng nơ-ron tích chập, chúng ta cần lướt qua một chút về các kiến thức toán học có liên quan đến phép tích chập. Chúng ta có thể hình dung một cách đơn giản rằng ý nghĩa của phép tích chập giống như một hoạt động trộn thông tin lại với nhau. Phép tích chập được ứng dụng tương đối rộng rãi trong nhiều ngành khoa học và kỹ thuật khác nhau.

Trong toán học, phép tích chập giữa hai hàm $f$ và $g$ sẽ tạo ra một hàm thứ ba biểu diễn sự biến đổi của của một hàm đối với hàm còn lại. Xét hai hàm $f$ và $g$, phép tích chập giữa hai hàm này được định nghĩa như sau:

\[h\left( x \right) = f \otimes g = \int\limits_{ - \infty }^\infty {f\left( {x - u} \right)} g\left( u \right)du = {F^{ - 1}}\left( {\sqrt {2\pi } F\left[ f \right]F\left[ g \right]} \right)\] \[\begin{array}{l} {\rm{feuture \thinspace map}} &= input \otimes kernel\\ &= \sum\limits_{y = 0}^{columns} {\left( {\sum\limits_{x = 0}^{rows} {input\left( {x - a,y - b} \right){\rm{kernel}}\left( {x,y} \right)} } \right)} \\ &= {F^{ - 1}}\left( {\sqrt {2\pi } F\left[ {input} \right]F\left[ {{\rm{kernel}}} \right]} \right) \end{array}\]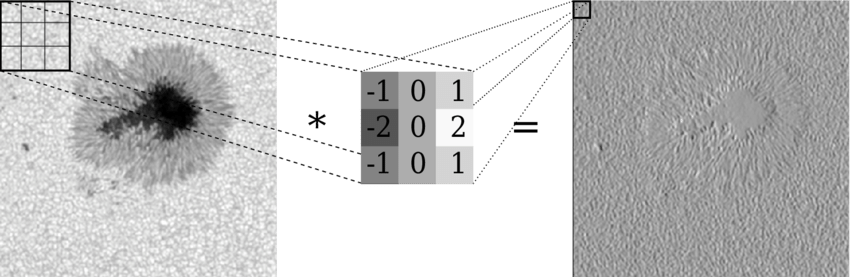

Chúng ta xem xét trong không gian một chiều, phép tích chập giữa hai hàm $f$ và $g$ được mô tả bởi phương trình sau:

\[\left( {f * g} \right)\left( x \right) = \sum\limits_t {f\left( t \right)} g\left( {x + t} \right)\]

Đối với dữ liệu đầu vào 2 chiều như hình ảnh, chúng ta có hai đầu vào cho phép tích chập. Đầu vào thứ nhất là một hình ảnh 2D, đầu vào còn lại được gọi là kernel hoặc mask hoạt động giống như bộ lọc (filter) cho hình ảnh 2D đầu vào và tạo ra một hình ảnh khác cho đầu ra. Chúng ta xem xét cụ thể một 2D-convolution sau:

\[\left( {K * I} \right)\left( {i,j} \right) = \sum\limits_{m,n} {K\left( {m,n} \right)} I\left( {i + n,j + m} \right)\]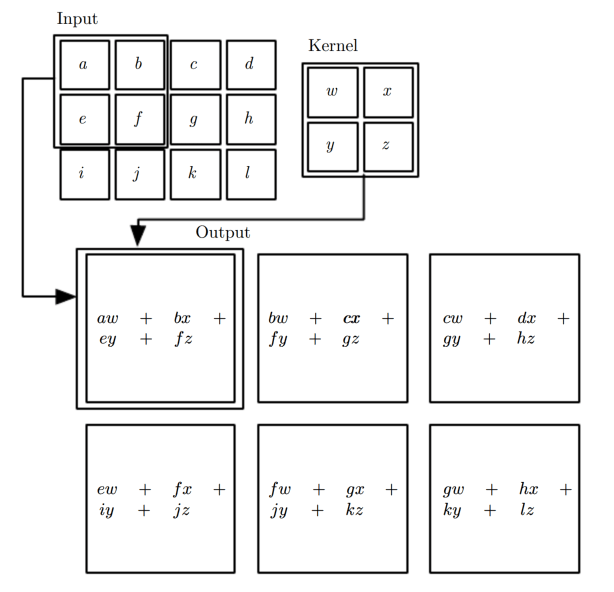

Convolutional Layer

Convolutional layer là một trong những thành phần quan trọng của mạng CNN. Nó có chức năng thực hiện phép tính convolutional trên input và trích xuất các feature từ dữ liệu đó. Convolutional layer nhận đầu vào là một tensor 3D (đối với ảnh RGB) hoặc 2D (đối với ảnh grayscale), sau đó áp dụng một bộ lọc convolutional (còn gọi là kernel hoặc filter) trên toàn bộ ảnh.

Bộ lọc này có thể được coi như một ma trận số thực kích thước nhỏ, có thể dịch chuyển trên toàn bộ ảnh để tạo ra các feature maps. Khi thực hiện phép tính convolution, các phần tử của bộ lọc nhân với các giá trị tương ứng của ảnh, và kết quả của phép nhân này được tổng hợp lại thành một giá trị duy nhất, được gọi là giá trị đầu ra của phép tính convolution tại vị trí tương ứng trên feature map.

Sau khi tính toán các giá trị đầu ra của phép tính convolution cho toàn bộ ảnh, chúng ta thu được một tập hợp các feature map, mỗi feature map đại diện cho một đặc trưng cụ thể của ảnh. Các feature map này được truyền vào một hàm kích hoạt (activation function) như ReLU để giúp tăng tính phi tuyến của mô hình và giảm thiểu độ lệch (bias).

Convolutional layer thường được sử dụng nhiều lần trong một mạng CNN để trích xuất các đặc trưng phức tạp và trừu tượng hơn. Ngoài ra, các convolutional layer còn có thể được kết hợp với các lớp khác như pooling layer để giảm kích thước của đầu vào và giúp mô hình hoạt động nhanh hơn.

Pooling Layer

Chức năng chung của pooling layer là giảm kích thước không gian của đặc trưng với mục đích chính là giảm số lượng tham số và khối lượng tính toán trong network, tăng tính tổng quát và hạn chế overfitting. Pooling layer hoạt động trên từng feuture map độc lập với nhau. Cơ chế hoạt động của pooling layer là chia nhỏ đầu vào thành các khối non-overlapping và áp dụng một hàm tóm tắt (summary function) trên mỗi khối để giảm kích thước đầu ra. Trong pooling layer, chúng ta có thể sử dụng nhiều loại pooling, trong đó max Pooling và average Pooling là hai loại phổ biến nhất.

Max Pooling

Kỹ thuật max pooling lấy giá trị lớn nhất từ mỗi vùng trượt của feature map và giữ lại giá trị này. Cụ thể, max pooling chia feature map thành các ô không giao nhau, mỗi ô có kích thước cố định (thường là 2x2 hoặc 3x3). Sau đó thì max pooling chọn giá trị lớn nhất trong mỗi ô và đưa ra đầu ra. Max Pooling giúp giữ lại đặc trưng quan trọng nhất của feature map và giảm số lượng tham số và tính toán trong mô hình.

Average Pooling

Kỹ thuật average pooling lấy giá trị trung bình từ mỗi vùng trượt của feature map và giữ lại giá trị này. Cụ thể, average pooling chia feature map thành các ô không giao nhau, mỗi ô có kích thước cố định (thường là 2x2 hoặc 3x3). Sau đó thì average pooling tính trung bình các giá trị trong mỗi ô và đưa ra đầu ra. Average pooling giúp giảm sự ảnh hưởng của nhiễu và giúp chúng ta thu được các thông tin trung bình từ feature map.

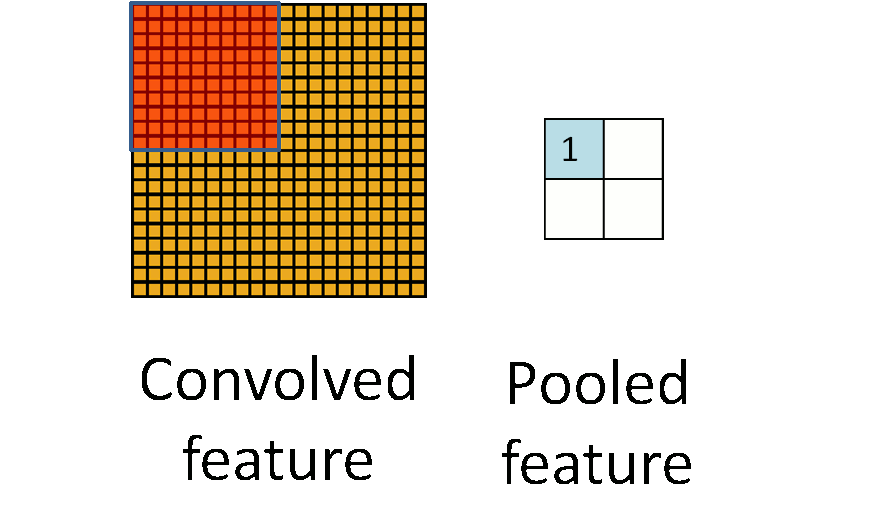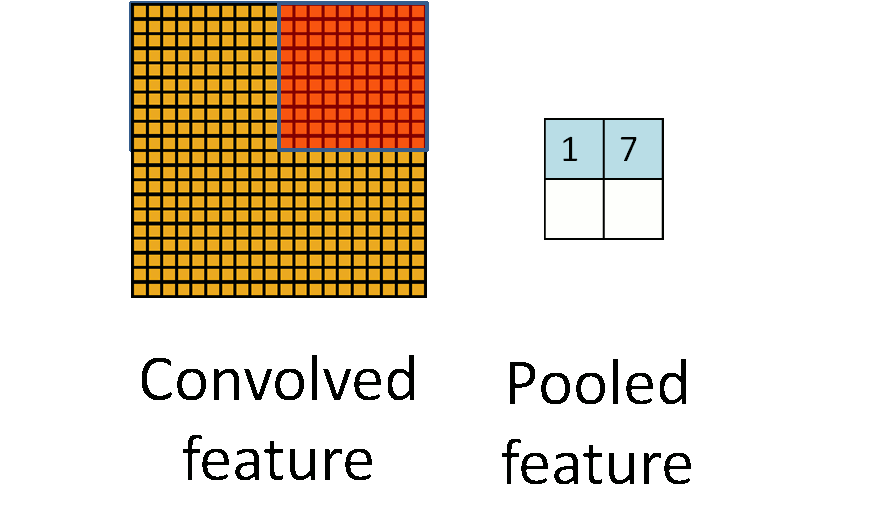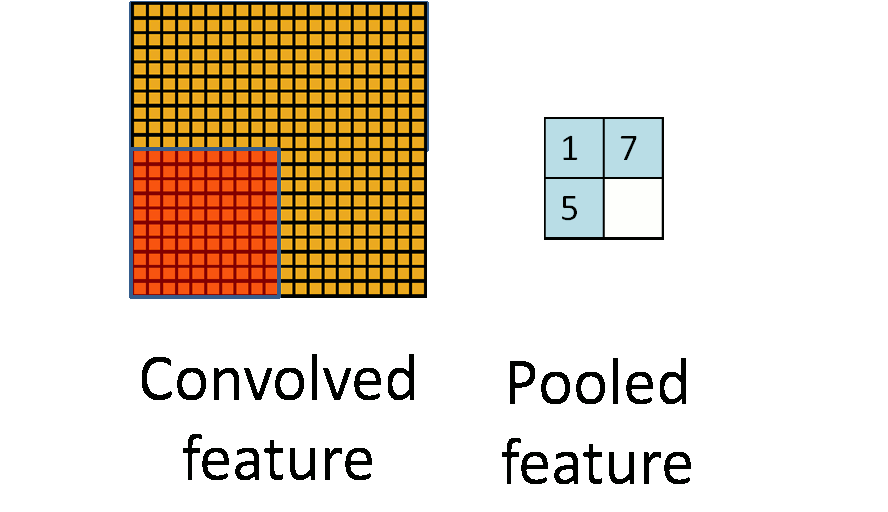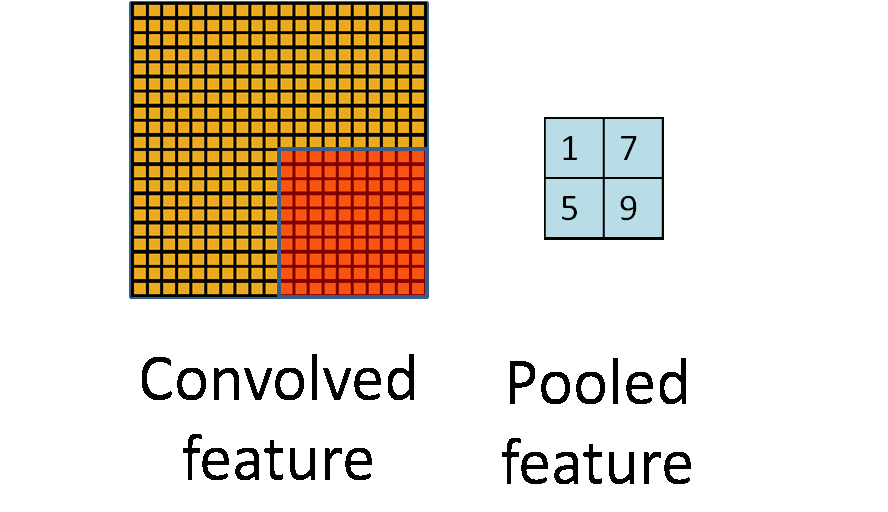
Cả max pooling và average pooling đều giúp giảm kích thước của feature map và tăng tốc độ tính toán của mô hình, giúp cho quá trình huấn luyện và dự đoán trên dữ liệu lớn trở nên hiệu quả hơn. Tuy nhiên thì max pooling thường được ưu tiên sử dụng hơn trong các ứng dụng thực tế vì nó giúp giữ lại các đặc trưng quan trọng của feature map hơn. Ví dụ cụ thể nếu ta có đầu vào là một ma trận kích thước 6x6, một max pooling với kernel size là 2x2 sẽ chia ma trận thành các khối 2x2 và lấy giá trị lớn nhất trong mỗi khối để tạo ra đầu ra kích thước 3x3. Max pooling có thể được sử dụng sau một convolutional layer để giảm kích thước đầu ra, tăng tốc độ tính toán và hạn chế overfitting.

Chúng ta có thể thấy pooling layer đóng các vai trò then chốt sau trong một mạng CNN:

• Giảm chiều sâu (depth) của đầu vào: Khi một pooling layer được áp dụng trên đầu ra của một convolutional layer, kích thước chiều sâu (depth) của đầu ra sẽ giảm đi. Điều này giúp giảm độ phức tạp của mô hình và giảm yêu cầu về tài nguyên tính toán.
• Tăng tính tổng quát của mô hình: Pooling layer có thể giúp tăng tính tổng quát của mô hình bằng cách giảm thông tin chi tiết về đặc trưng, tạo ra đặc trưng trừu tượng hơn.
• Hạn chế overfitting: Pooling layer có thể giúp hạn chế overfitting bằng cách loại bỏ các đặc trưng không cần thiết hoặc không quan trọng trong đầu vào, từ đó giúp mô hình dự đoán tốt hơn trên dữ liệu mới.

Fully connected layer

Fully connected layer là lớp cuối cùng trong mạng CNN có chức năng thực hiện việc phân loại hoặc dự đoán các giá trị đầu ra của mô hình. Convolutional layer và pooling layer đã thực hiện các phép tích chập và giảm kích thước của dữ liệu đầu vào, tạo ra các đặc trưng cục bộ cho ảnh. Tuy nhiên thì chúng chỉ tạo ra các đặc trưng cục bộ và không liên kết các đặc trưng đó để đưa ra một dự đoán cuối cùng. Để phân loại chính xác hơn, chúng ta cần kết nối tất cả các đặc trưng đó với nhau và tính toán xác suất cho các lớp đầu ra. Fully connected layer trong mạng CNN được thiết kế có một số nơ-ron kết nối với tất cả các nơ-ron trong lớp trước đó (có thể là một lớp convolutional layer hoặc pooling layer) để nhận đầu vào là tất cả các đặc trưng từ lớp trước đó. Fully connected layer lúc này có nhiệm vụ kết nối các đặc trưng cục bộ đã được trích xuất từ các lớp convolutional layer và pooling layer để đưa ra một dự đoán cuối cùng.

Fully connected layer giúp mạng CNN học các mối quan hệ phức tạp giữa các đặc trưng đầu vào và tạo ra các phân loại chính xác hơn. Tuy nhiên khi sử dụng quá nhiều fully connected layer trong một mạng CNN sẽ dẫn đến hiện tượng overfitting, khi mô hình chỉ học nhớ dữ liệu huấn luyện mà không có khả năng dự đoán đúng trên các dữ liệu mới. Do đó số lượng fully connected layer cần được cân nhắc để tối ưu hóa hiệu suất của mạng CNN.

Thành tựu

CNN là một trong những phát triển đáng chú ý nhất trong lĩnh vực học sâu và đã đạt được nhiều thành tựu quan trọng trong nhiều mảng khác nhau. Trong các bài toán có liên quan đến hình ảnh như nhận dạng hình ảnh (image recognition) và phân lớp hình ảnh (image classification) hiện nay, mạng CNN có những ứng dụng tiêu biểu sau:

• Phân loại ảnh: CNN được sử dụng rộng rãi để phân loại ảnh, từ việc phát hiện khuôn mặt đến phân loại các loài động vật hoang dã.
• Tự động lái xe: CNN cũng được sử dụng để xử lý dữ liệu từ các cảm biến trên ô tô và giúp xe tự lái tránh các vật cản và điều khiển tốc độ.
• Phát hiện bệnh: CNN đã được sử dụng để phát hiện các bệnh lý y tế từ các hình ảnh y khoa, giúp các chuyên gia y tế phát hiện sớm các bệnh trước khi chúng trở nên nghiêm trọng hơn.
• Truy vấn hình ảnh: CNN cũng đã được sử dụng để truy vấn hình ảnh, cho phép người dùng tìm kiếm các hình ảnh dựa trên các thông tin liên quan đến nó.

Ngoài ra thì mạng CNN còn được ứng dụng trong các bài toán xử lý ngôn tự nhiên (natural language processing) như phát hiện thư rác (spam detection), phân loại văn bản (topic categorization),…

Tài liệu tham khảo