Giải thích chi tiết về mạng Long Short-Term Memory (LSTM)
Giới thiệu về Recurrent Neural Network
Trước khi đi sâu vào giải thích chi tiết mạng LSTM, mình sẽ giới thiệu sơ qua về mạng nơ-ron hồi quy (Recurrent Neural Network - RNN). Đây là mạng nơ-ron nhân tạo được thiết kế cho việc xử lý các loại dữ liệu có dạng chuỗi tuần tự.
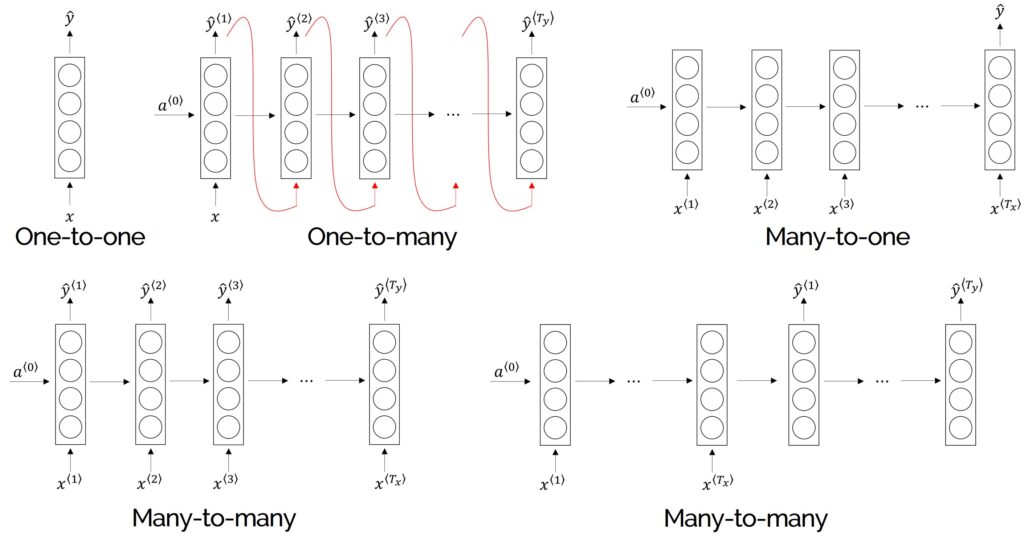
Dựa trên số lượng xử lý của chuỗi đầu vào và chuỗi đầu ra, người ta chia mạng RNN thành 4 loại chính:
- One to One RNN
- One to Many RNN
- Many to One RNN
- Many to Many RNN
Trong mạng RNN, trạng thái ẩn tại mỗi bước thời gian sẽ được tính toán dựa vào dữ liệu đầu vào tại bước thời gian tương ứng và các thông tin có được từ bước thời gian trước đó, tạo khả năng ghi nhớ các thông tin đã được tính toán ở những bước thời gian trước cho mạng. Hình 2 biễu diễn kiến trúc của một mạng RNN cơ bản cho tác vụ ánh xạ một chuỗi đầu vào thành chuỗi đầu ra với cùng một độ dài khi được duỗi ra.
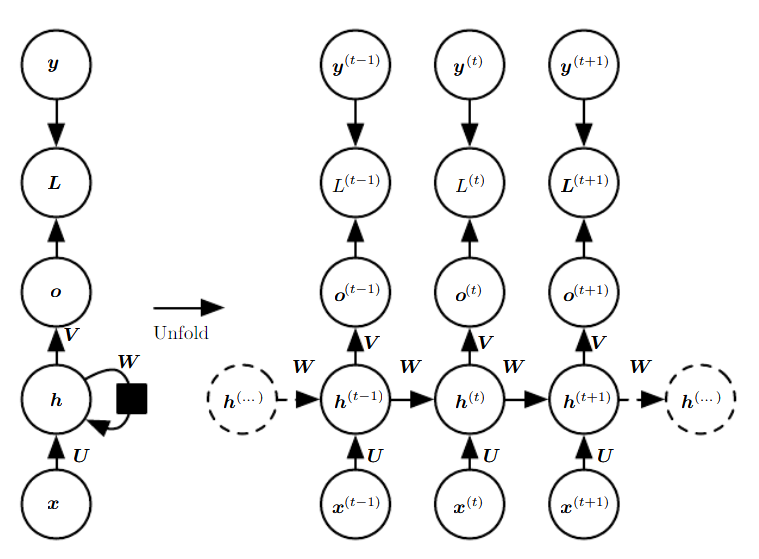
Trong Hình 1, xét tại mỗi bước thời gian $t$ theo chiều từ dưới lên trên, \({x^{\left( t \right)}}\) là giá trị đầu vào, \({h^{\left( t \right)}}\) là trạng thái ẩn, \({o^{\left( t \right)}}\) là giá trị đầu ra. $U$, $W$, $V$ là các ma trận trọng số của mạng RNN. $L$ là hàm tính mất mát giữa giá trị đầu ra \({o^{\left( t \right)}}\) từ mạng RNN và giá trị đầu ra chuẩn \({y^{\left( t \right)}}\) từ tập dữ liệu.
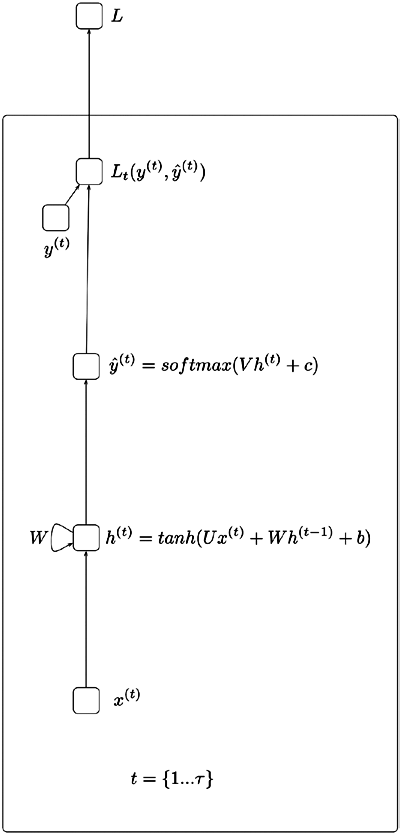
Đi sâu vào kiến trúc chi tiết hơn, chúng ta xem các vector \({x^{\left( 1 \right)}},{x^{\left( 2 \right)}},...,{x^{\left( \tau \right)}}\) đại diện cho các phần tử trong chuỗi dữ liệu đầu vào, tại mỗi bước thời gian $t$, mạng RNN nhận lần lượt từng vector $x^{(t)}$ và thực hiện những tính toán để ánh xạ thành chuỗi đầu ra được mô tả bởi các phương trình sau:
\[\begin{align} &{h^{\left( t \right)}} = \tanh \left( {U{x^{\left( t \right)}} + W{h^{\left( {t - 1} \right)}} + b} \right)\\ &{o^{\left( t \right)}} = V{h^{\left( t \right)}} + c\\ &\hat{y}^{(t)} = {\rm{softmax}}\left( {{o^{\left( t \right)}}} \right)\\ \end{align}\]Trong đó:
- $x^{(t)}$: Giá trị đầu vào tại bước thời gian $t$
- $h^{(t)}$: Trạng thái ẩn tại bước thời gian $t$
- $o^{(t)}$: Giá trị đầu ra tại bước thời gian $t$
- $\hat{y}^{(t)}$: Vector xác suất đã chuẩn hóa qua hàm softmax tại bước thời gian $t$
- $U$, $V$, $W$: Các ma trận trọng số trong mạng RNN tương ứng với các kết nối theo chiều lần lượt là từ đầu vào đến trạng thái ẩn, từ trạng thái ẩn đến đầu ra và từ trạng thái ẩn đến trạng thái ẩn
- $b$, $c$: Độ lệch (bias)
Các vấn đề về gradient trong quá trình huấn luyện
Gradient biến mất (Vanishing Gradient Problem) và gradient bùng nổ (Exploding Gradient Problem) là những vấn đề gặp phải khi sử dụng các kỹ thuật tối ưu hóa trọng số dựa trên gradient để huấn luyện mạng nơ-ron. Các vấn đề này thường gặp phải do việc lựa chọn các hàm kích hoạt không hợp lý hoặc số lượng các lớp ẩn của mạng quá lớn. Đặc biệt, các vấn đề này thường hay xuất hiện trong quá trình huấn luyện các mạng nơ-ron hồi quy. Trong thuật toán BPTT, khi chúng ta càng quay lùi về các bước thời gian trước đó thì các giá trị gradient càng giảm dần, điều này làm giảm tốc độ hội tụ của các trọng số do sự thay đổi hầu như rất nhỏ. Trong một số trường hợp khác, các gradient có giá trị rất lớn khiến cho quá trình cập nhật các trọng số bị phân kỳ và vấn đề này được gọi là gradient bùng nổ. Các vấn đề về gradient biến mất thường được quan tâm hơn vấn đề gradient bùng nổ do vấn đề gradient biến mất khó có thể được nhận biết trong khi gradient bùng nổ có thể dễ dàng quan sát và nhận biết hơn. Có nhiều nghiên cứu đề xuất các giải pháp để giải quyết những vấn đề này như lựa chọn hàm kích hoạt hợp lý, thiết lập các kích thước cho mạng hợp lý hoặc khởi tạo các trọng số ban đầu phù hợp khi huấn luyện. Một trong các giải pháp cụ thể có thể chỉ ra là thuật toán Truncated BPTT, một biến thể cải tiến của BPTT được áp dụng trong quá trình huấn luyện mạng nơ-ron hồi quy trên các chuỗi dài. Ngoài ra, cơ chế của mạng LSTM được đề xuất đã khắc phục được các vấn đề này sẽ được giới thiệu trong phần tiếp theo.
Mạng RNN bị ảnh hưởng bởi khả năng ghi nhớ ngắn hạn (short-term memory). Nếu dữ liệu đầu vào là một chuỗi trình tự dài, mạng RNN sẽ gặp khó khăn trong việc chuyển tải thông tin từ các bước thời gian đầu tiên đến các bước sau đó. Ví dụ trong bài toán phân loại văn bản, nếu chúng ta đang cố gắng xử lý một đoạn văn bản dài để thực hiện phân loại, mạng RNN có thể bỏ sót nhiều thông tin quan trọng ngay từ những bước đầu.
Cơ chế hoạt động của mạng LSTM
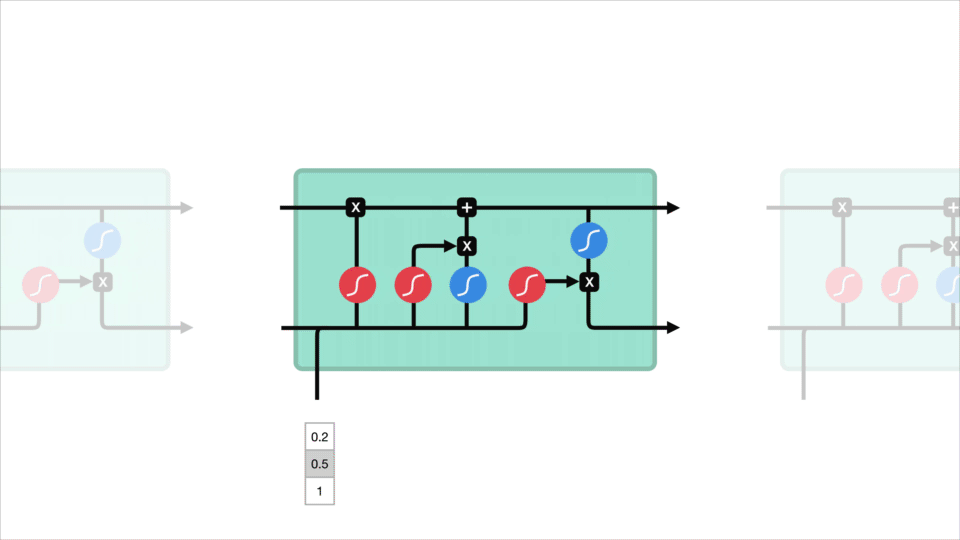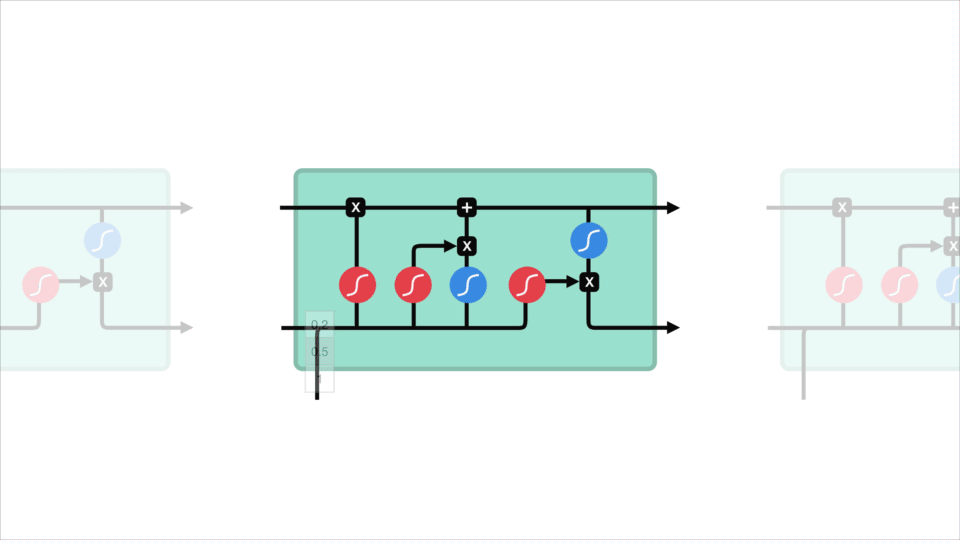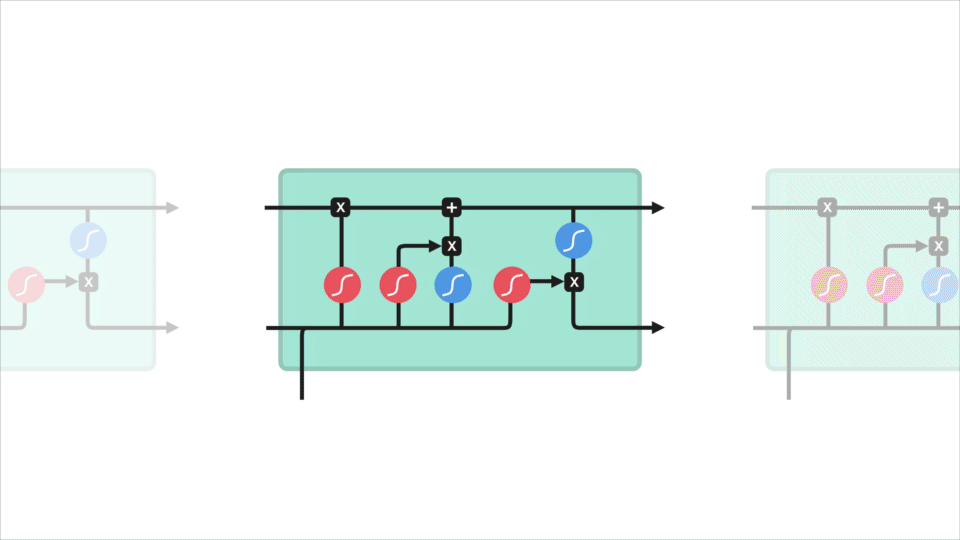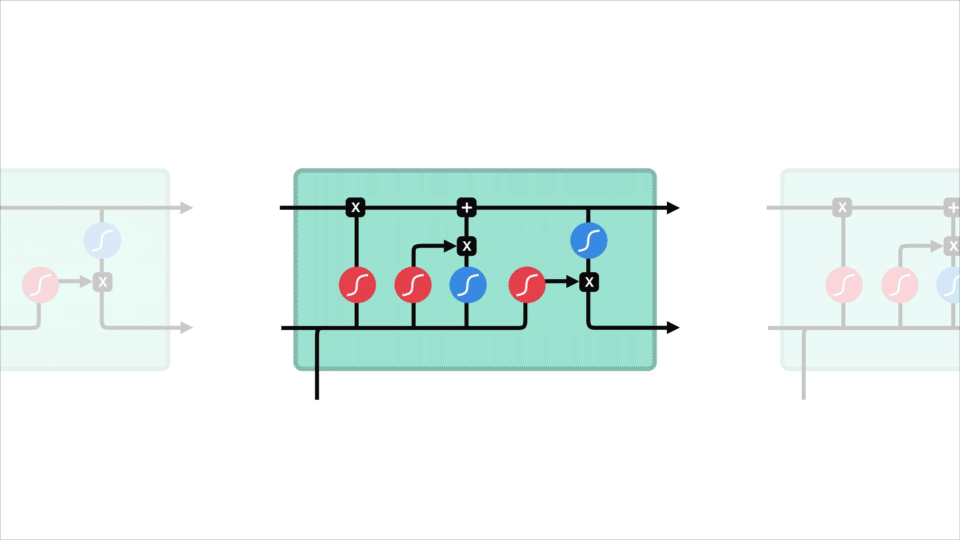
LSTM là một phiên bản mở rộng của mạng RNN, được đề xuất vào năm 1997 bởi Sepp Hochreiter và Jürgen Schmidhuber. LSTM được thiết kế để giải quyết các bài toán về phụ thuộc xa (long-term dependencies) trong mạng RNN do bị ảnh hưởng bởi vấn đề gradient biến mất.
Giả sử khi xem một bộ phim dài tập, chúng ta ghi nhớ bối cảnh phim đã diễn ra ở những tập trước đó, kết hợp xử lý với thông tin của tập phim hiện tại hoặc khi đọc sách, chúng ta ghi nhớ điều gì đã xảy ra ở chương trước, kết hợp thành mạch thông tin để hiểu và tiếp thu cho nội dung hiện tại. Tương tự như vậy, khi các mạng RNN hoạt động, thông tin trước đó được ghi nhớ và sử dụng lại để xử lý cho đầu vào hiện tại. Tuy nhiên thì mạng RNN không thể ghi nhớ thông tin ở các bước có khoảng cách khá xa trước đó do vấn đề gradient biến mất. Do đó những phần tử đầu tiên trong chuỗi đầu vào không có nhiều ảnh hưởng đến các kết quả tính toán dự đoán phần tử cho chuỗi đầu ra trong các bước sau. Mạng LSTM với các kết nối phản hồi (feedback connection) giúp khắc phục nhược điểm này.
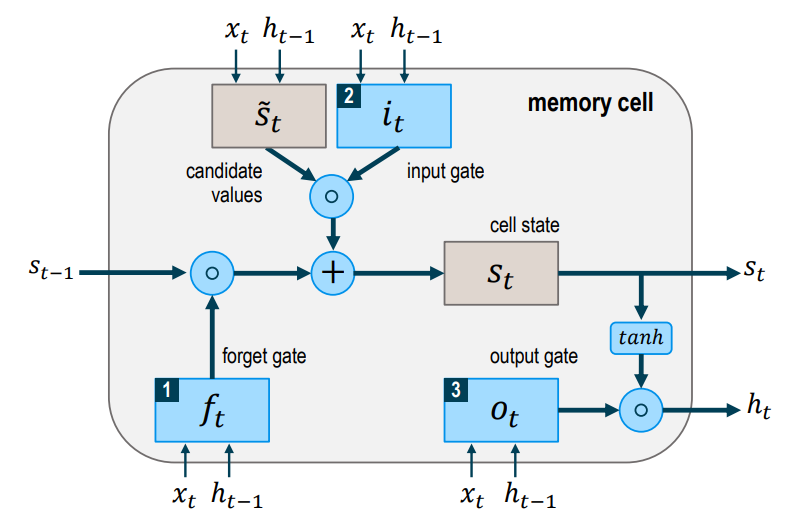
Mạng LSTM có thể bao gồm nhiều tế bào LSTM (LSTM memory cell) liên kết với nhau và kiến trúc cụ thể của mỗi tế bào được biểu diễn như trong Hình 2. Ý tưởng của LSTM là bổ sung thêm trạng thái bên trong tế bào (cell internal state) \(s_t\) và ba cổng sàng lọc các thông tin đầu vào và đầu ra cho tế bào bao gồm forget gate \({f_t}\), input gate \({i_t}\) và output gate \({o_t}\). Tại mỗi bước thời gian $t$, các cổng đều lần lượt nhận giá trị đầu vào ${x_t}$ (đại diện cho một phần tử trong chuỗi đầu vào) và giá trị $ {h_{t - 1}} $ có được từ đầu ra của memory cell từ bước thời gian trước đó $t-1$. Các cổng đều đóng vai trò có nhiệm vụ sàng lọc thông tin với mỗi mục đích khác nhau:
- Forget gate: Có nhiệm vụ loại bỏ những thông tin không cần thiết nhận được khỏi cell internal state
- Input gate: Có nhiệm vụ chọn lọc những thông tin cần thiết nào được thêm vào cell internal state
- Output gate: Có nhiệm vụ xác định những thông tin nào từ cell internal state được sử dụng như đầu ra
Trước khi trình bày các phương trình mô tả cơ chế hoạt động bên trong của một tế bào LSTM, chúng ta sẽ thống nhất quy ước một số ký hiệu được sử dụng sau đây:
-
${x_{t}}$ là vector đầu vào tại mỗi bước thời gian $t$
-
\({W_{f,x}},{W_{f,h}},{W_{\mathop s\limits^ \sim ,x}},{W_{\mathop s\limits^ \sim ,h}},{W_{i,x}},{W_{i,h}},{W_{o,x}},{W_{o,h}}\) là các ma trận trọng số trong mỗi tế bào LSTM.
-
\({b_f},{b_{\mathop s\limits^ \sim }},{b_i},{b_o}\) là các vector bias.
-
\({f_t},{i_t},{o_t}\) lần lượt chứa các giá trị kích hoạt lần lượt cho các cổng forget gate, input gate và output gate tương ứng.
-
\({s_t},\mathop s\limits^ \sim\) lần lượt là các vector đại diện cho cell internal state và candidate value.
-
${h_{t}}$ là giá trị đầu ra của tế bào LSTM.
Trong quá trình lan truyền xuôi (forward pass), cell internal state \({s_t}\) và giá trị đầu ra ${h_{t}}$ được tính như sau:
-
Ở bước đầu tiên, tế bào LSTM quyết định những thông tin nào cần được loại bỏ từ cell internal state ở bước thời gian trước đó \({s_{t - 1}}\). Activation value \({f_{t}}\) của forget gate tại bước thời gian $t$ được tính dựa trên giá trị đầu vào hiện tại \({x_{t}}\), giá trị đầu ra \({h_{t-1}}\) từ tế bào LSTM ở bước trước đó và bias \({b_f}\) của forget gate. Hàm sigmoid function biến đổi tất cả activation value về miền có giá trị trong khoảng từ $0$ (hoàn toàn quên) và $1$ (hoàn toàn ghi nhớ):
\[\begin{equation} {f_t} = \sigma \left( {{W_{f,x}}{x_t} + {W_{f,h}}{h_{t - 1}} + {b_f}} \right) \end{equation}\] -
Ở bước thứ hai, tế bào LSTM quyết định những thông tin nào cần được thêm vào cell internal state \({s_{t}}\). Bước này bao gồm hai quá trình tính toán đối với \(\mathop {{s_t}}\limits^ \sim\) và \({f_{t}}\). Candidate value \(\mathop {{s_t}}\limits^ \sim\) biểu diễn những thông tin tiềm năng cần được thêm vào cell internal state được tính như sau:
\[\begin{equation} \mathop {{s_t}}\limits^ \sim = \tanh \left( {{W_{\mathop s\limits^ \sim ,x}}{x_t} + {W_{\mathop s\limits^ \sim ,h}}{h_{t - 1}} + {b_{\mathop s\limits^ \sim }}} \right) \end{equation}\]Activation value \({i_t}\) của input gate theo đó cũng được tính như sau:
\[\begin{equation} {i_t} = \tanh \left( {{W_{i,x}}{x_t} + {W_{i,h}}{h_{t - 1}} + {b_i}} \right) \end{equation}\] -
Ở bước thứ ba, giá trị mới của cell internal state \({s_{t}}\) được tính dựa trên kết quả tính toán thu được từ các bước trước với phép nhân Hadamard theo từng phần tử (Hadamard product) được ký hiệu bằng \(\circ\):
\[\begin{equation} {s_t} = {f_t} \circ {s_{t - 1}} + {i_t} \circ \mathop {{s_t}}\limits^ \sim \end{equation}\] -
Ở bước cuối cùng, giá trị đầu ra \({h_{t}}\) của tế bào LSTM được tính toán dựa theo hai phương trình sau:
\[\begin{equation} {o_t} = \sigma \left( {{W_{o,x}}{x_t} + {W_{o,h}}{h_{t - 1}} + {b_o}} \right) \end{equation}\] \[\begin{equation} {h_t} = {o_t} \circ \tanh \left( {{s_t}} \right) \end{equation}\]
