Hệ thống mật mã khóa công khai RSA
RSA được đặt tên dựa theo tên của những người phát minh ra nó là Ronald L. Rivest, Adi Shamir và Leonard M. Adleman. Những người này đã tạo ra hệ thống mật mã khóa công khai RSA (public-key cryptography) khi họ còn đang làm việc tại Viện Công nghệ Massachusetts (MIT). Trong phạm vi của bài viết này, mình sẽ trình bày về ý tưởng cơ chế hoạt động của hệ thống mật mã khóa công khai RSA, các cơ sở lý thuyết toán học trong quá trình mã hóa và giải mã thông điệp cùng với ví dụ minh họa cụ thể.
Ý tưởng và nguyên lý
Thuật toán RSA (RSA algorithm) được xây dựng dựa trên ý tưởng cho rằng thao tác thực hiện phép tích với các thừa số có kích thước lớn cho trước là rất dễ dàng, nhưng phân tích một số cho trước có kích thước lớn thành các thừa số là rất khó khăn. Ví dụ quá trình thực hiện phép nhân 571 với 997 rất mau chóng cho ra kết quả là 569.287. Nhưng quá trình phân tích 569.287 thành các thừa số thì không dễ dàng như vậy.
Cơ chế hoạt động
Để mọi người có thể dễ hiểu hơn, mình sẽ dùng một ví dụ cụ thể sau đây để giải thích về cơ chế hoạt động của mật mã RSA. Giả sử Alice muốn gửi cho Bob một món đồ quý giá nhưng không muốn bị người khác có thể biết được.
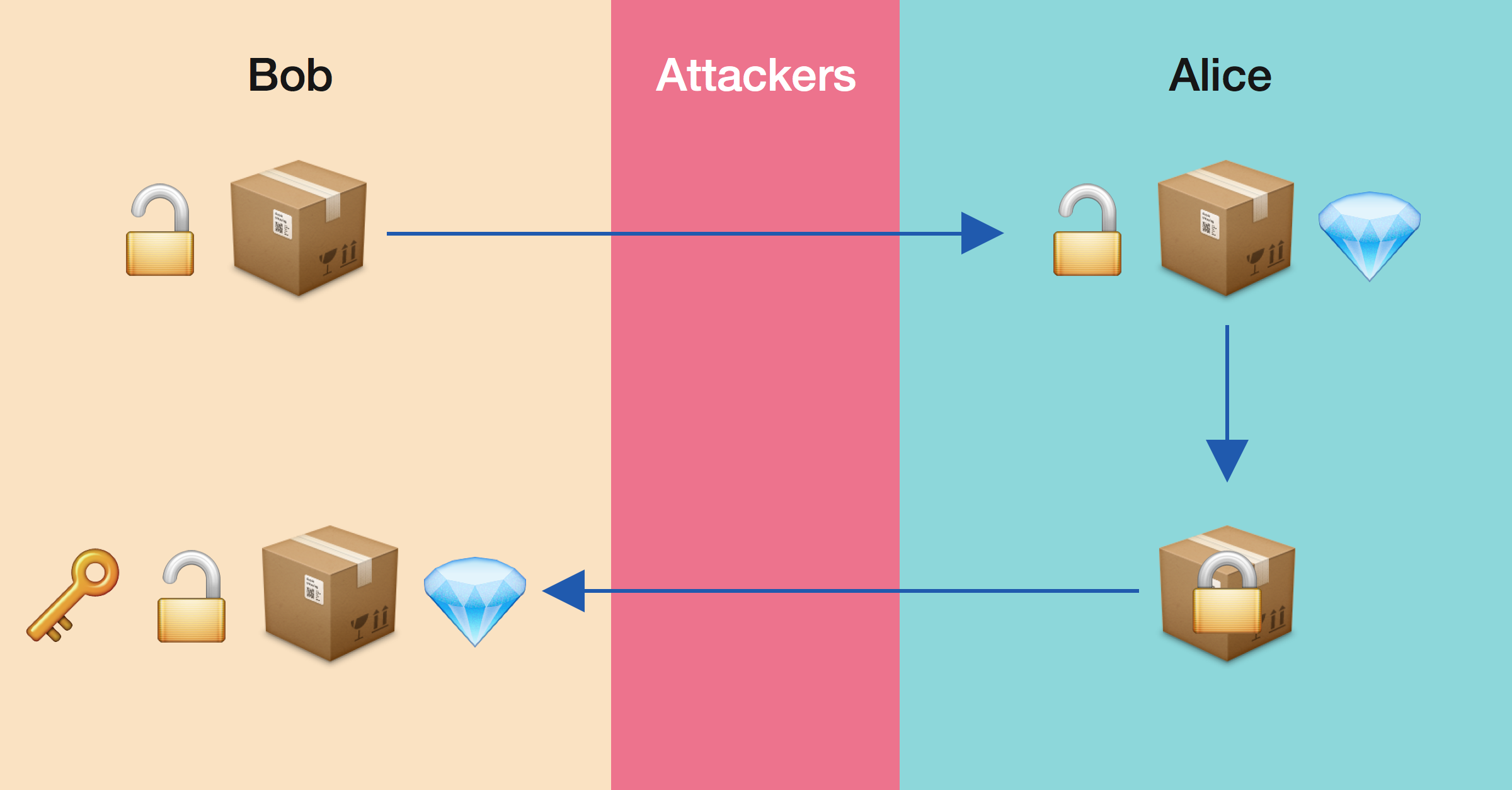
- Đầu tiên Bob gửi cho Alice một ổ khóa kèm chiếc rương đã mở khóa. Bob sẽ giữ lại chìa khoá tương ứng cho ổ khoá này và không gửi nó cho bất kỳ ai.
- Alice sau khi nhận ổ khoá kèm chiếc rương từ Bob sẽ bỏ món đồ cần gửi vào rương và bấm khoá lại. Ngay cả Alice sau khi bấm khoá cũng không thể tự mở khoá ra.
- Alice sau đó gửi chiếc rương đã khoá lại có món đồ bên trong cho Bob.
- Bob nhận chiếc rương này sẽ dùng chìa khoá tương ứng ban đầu để mở khoá ra và lấy món đồ trong rương.
Ví dụ này thể hiện những ý tưởng về cơ chế hoạt động của mật mã khóa công khai, mặc dù trên thực tế có hơi khác một chút. Trong RSA, Alice mã hóa thông điệp (message) của mình bằng khóa công khai (public key) của Bob. Thông điệp đã mã hoá bằng khoá này chỉ có thể được giải mã bằng khóa riêng tư (private key) của Bob.
Khóa công khai được tạo bằng cách nhân hai số nguyên tố lớn \(p\) và \(q\) với nhau. Khóa riêng tư được tạo thông qua một quy trình khác liên quan đến \(p\) và \(q\). Bên cần trao đổi thông điệp sau đó có thể phân phối khóa công khai \(pq\) của mình cho bất kỳ bên nào muốn gửi thông điệp và giữ lại khoá riêng tư. Bên gửi thông điệp sẽ mã hóa thông điệp của họ bằng khóa công khai trước khi gửi đi.
Tạo cặp khóa trong RSA
Một cặp khóa công khai (public key) và khóa riêng tư (private key) trong mật mã RSA có thể được tạo thành thông qua các bước sau đây:
- Tạo ra ngẫu nhiên một cặp số nguyên tố $p$ và $q$ có kích thước rất lớn.
- Tính $n$ với \(n = pq\).
- Chọn ra một số mũ lẻ công khai (odd public exponent) $e$ có giá trị từ $3$ đến $n-1$ mà nguyên tố cùng nhau (coprime) với $p-1$ và $q-1$.
- Tính toán số mũ bí mật (private exponent) $d$ từ $e, p$ và $q$ với e thỏa mãn \(de \equiv 1\,\,\left( {\bmod \,L} \right)\), trong đó \(L = LCM\left( {p - 1,q - 1} \right)\).
- Gán \(public\,key = (n, e)\) và \(private\,key = (n, d)\).
Mã hóa nội dung trong RSA
Giả sử ta có một thông điệp \(m\) cần được mã hóa thành ciphertext \(c\) trước khi gửi đi, khi đó:
\[\begin{align} c = ENCRYPT\left( m \right) = {m^e}\bmod n \end{align}\]Giải mã nội dung trong RSA
Khi người nhận cần giải mã thông điệp đã được mã hóa \(c\) thành lại thông điệp gốc ban đầu \(m\), hàm giải mã sẽ được thực hiện như sau:
\[\begin{align} m = DECRYPT\left( c \right) = {c^d}\bmod n \end{align}\]Cơ sở toán học
-
Rất dễ để thực hiện quá trình tìm một số nguyên tố ngẫu nhiên với kích thước cho trước.
-
Cho 2 số \(p\) và \(q\), quá trình tính tích \(n = pq\) luôn được thực hiện dễ dàng.
-
Cho số \(n\), quá trình tìm lại các thừa số nguyên tố \(p\) và \(q\) là rất khó.
-
Cho các số \(m\), \(n\) và \(e\), quá trình tính \(c = {m^e}\,\bmod \,n\) luôn được thực hiện dễ dàng.
-
Cho các số \(n, e, c\) và các thừa số nguyên tố \(p\) và \(q\), quá trình tìm \(m\) sao cho thỏa mãn \(c = {m^e}\,\bmod \,n\) luôn được thực hiện dễ dàng.
-
Chỉ cung cấp các số \(n, e, c\) nhưng không cung cấp các thừa số nguyên tố \(p\) và \(q\), quá trình tìm \(m\) sao cho thỏa mãn \(c = {m^e}\,\bmod \,n\) là không dễ dàng.
Ứng dụng của mã hoá RSA
Trong mật mã RSA, cả khóa công khai và khóa riêng tư đều có thể mã hóa nội dung. Nếu một khoá được sử dụng để mã hoá nội dung thì khoá còn lại được dùng để giải mã nội dung. Thuộc tính này là một lý do tại sao RSA trở thành thuật toán bất đối xứng (asymmetric cryptography) được sử dụng rộng rãi nhất. Nó cung cấp phương pháp đảm bảo tính bí mật, tính toàn vẹn, tính xác thực và tính không thể chối bỏ (non-repudiation) của truyền thông điện tử.
Nhiều giao thức bao gồm Secure Shell (SSH), OpenPGP, S/MIME và SSL/TLS đều dựa vào mã hoá RSA cho các chức năng mã hóa và chữ ký số. Nó cũng được sử dụng trong các trình duyệt để thiết lập một kết nối an toàn qua các mạng không an toàn. Xác minh chữ ký RSA là một trong những hoạt động được thực hiện phổ biến nhất trong các hệ thống kết nối mạng.
