Biological Neural Network

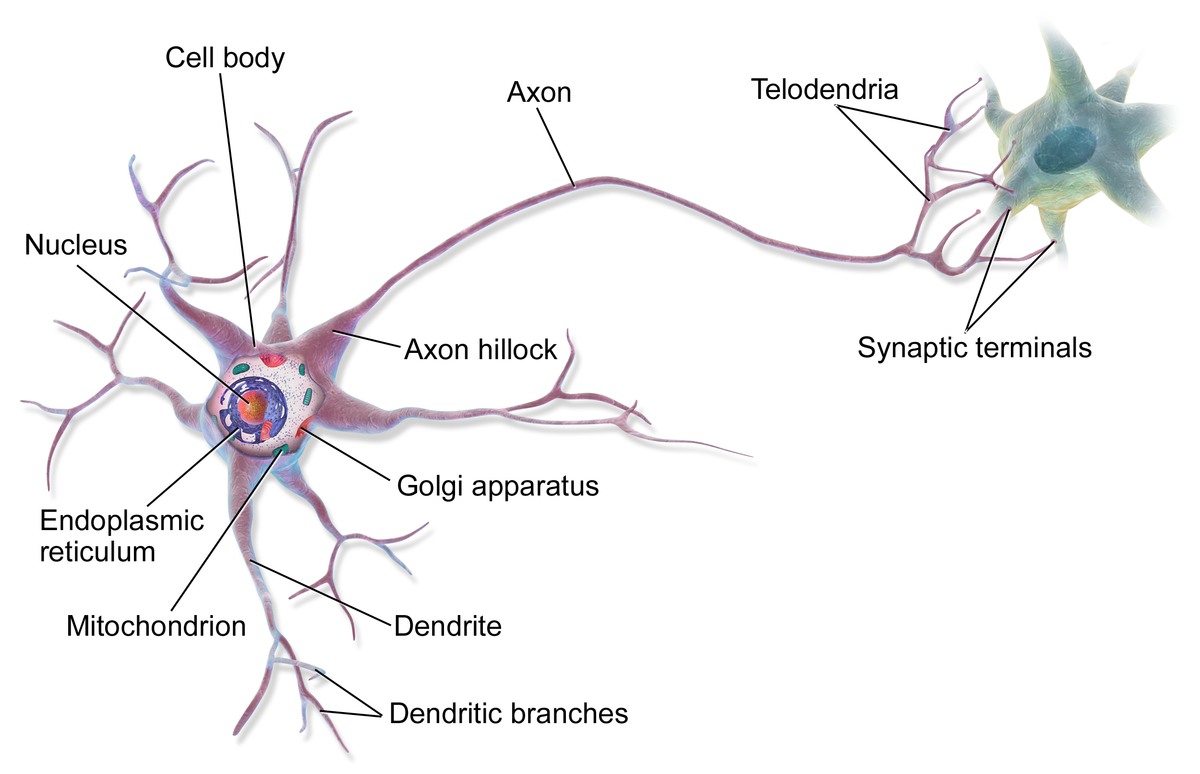
Những ý tưởng xây dựng các mô hình mạng nơ-ron nhân tạo bắt nguồn từ việc khám phá ra các cơ chế hoạt động đơn giản của mạng nơ-ron sinh học (biological neural network). Trong hệ thống thần kinh sinh học, nơ-ron là tế bào sống và còn là đơn vị lưu trữ cơ bản trong bộ não của con người. Có khoảng 200 tỉ nơ-ron trong bộ não con người. Mỗi nơ-ron được liên kết với khoảng từ 1.000 đến 10.000 nơ-ron khác thông qua các khớp thần kinh (synapse). Các tín hiệu xung điện được truyền từ tế bào nơ-ron này sang tế bào nơ-ron khác thông qua các khớp thần kinh. Có tất cả khoảng 125 nghìn tỉ khớp thần kinh trong bộ não của con người.

Bộ não của con người lưu trữ thông tin trong những tế bào thần kinh và những khớp thần kinh giữa các tế bào này với nhau. Mỗi khái niệm trong não có thể được tượng trưng bằng một mạng của các kết nối khác nhau giữa những tế bào thần kinh. Sự hình thành các kiến thức mới (learning) xảy ra khi các khớp kết nối giữa nhiều nơ-ron trở nên mạnh hơn và liên kết giữa một cụm tế bào mới được hình thành. Cụ thể hơn là những thông tin này được hình thành từ khả năng thay đổi cường độ liên kết giữa các khớp thần kinh hay còn được gọi là sự mềm dẻo của khớp thần kinh (synaptic plasticity). Giả thuyết này được đưa ra bởi Hebb vào năm 1949, người cho rằng sự mềm dẻo của khớp thần kinh được tạo ra từ những kích thích lặp đi lặp lại và kéo dài giữa khớp tế bào trước (presynaptic terminal) và khớp tế bào sau (postsynaptic terminal). Điều này có nghĩa là khi hai nơ-ron được kích hoạt cùng lúc, các khớp thần kinh giữa hai tế bào sẽ trở nên mạnh hơn và hai tế bào này sẽ có thể kích hoạt lẫn nhau hiệu quả hơn. Các quá trình kích hoạt tạo sự liên kết này lâu dần sẽ tạo ra mạng lưới của các kết nối và nó sẽ đại diện cho một khái niệm nào đó.

Artificial Neural Network

Các nhà nghiên cứu đã tìm cách chuyển đổi những hiểu biết về cách thức hoạt động của các tế bào thần kinh sinh học thành các mô hình mạng nơ-ron nhân tạo (Artificial Neural Network) có thể hoạt động được trên máy tính. Hình bên dưới cho thấy mô hình của một nơ-ron đơn lẻ, được xem như đơn vị xử lý thông tin cơ bản của một mạng nơ-ron. Các nơ-ron này được sử dụng để xây dựng thành các mạng nơ-ron có kiến trúc phức tạp hơn sẽ được trình bày trong các phần sau. Chúng ta sẽ xem xét 3 thành phần cơ bản của một mạng nơ-ron:

• Một tập hợp các khớp thần kinh (synapse) hoặc còn được gọi là connecting link dùng để kết nối các nơ-ron lại với nhau. Mỗi khớp thần kinh được đặc trưng bởi cường độ liên kết của nó. Cụ thể hơn, một khớp thần kinh dùng để chuyển tín hiệu từ nơ-ron có nhãn $j$ sang nơ-ron có nhãn $k$ với trọng số là \({{w_{kj}}}\). Không giống như trọng số của một khớp thần kinh trong hệ thần kinh sinh học, trọng số của một khớp thần kinh nhân tạo có thể mang giá trị âm hoặc dương.
• Một bộ cộng (adder) dùng để tổng hợp các tín hiệu đầu vào tại mỗi nơ-ron và gửi kết quả đi tiếp.
• Một hàm kích hoạt (activation function) dùng để đưa các tín hiệu đầu ra của nơ-ron vào một miền giá trị nhất định hoặc vào một tập hợp các giá trị cố định.

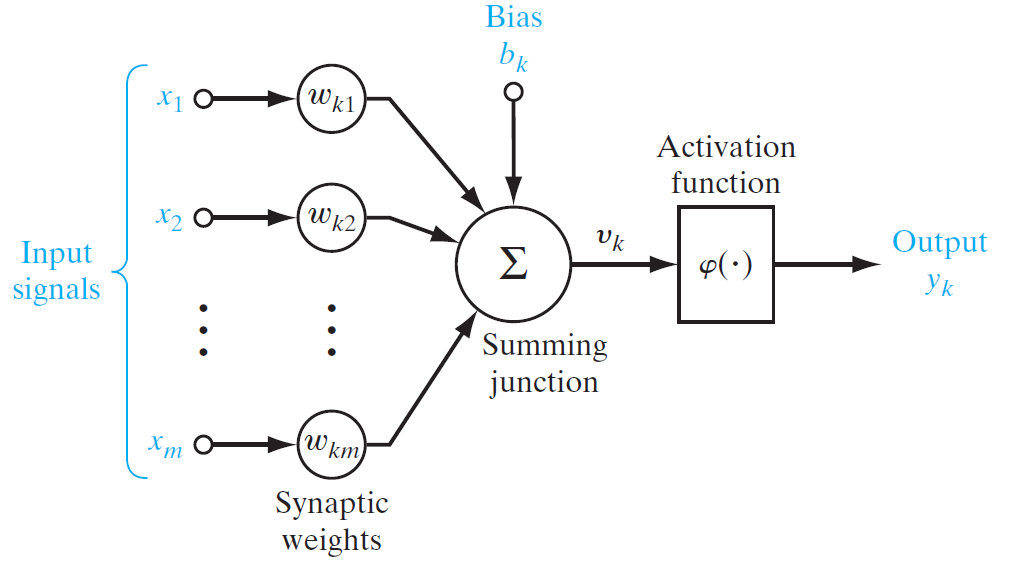
Chúng ta có thể mô tả hoạt động của nơ-ron có nhãn $k$ trong hình trên bằng các phương trình toán học như sau:

\[\begin{align} &{u_k} = \sum\limits_{j = 1}^m {{w_{kj}}{x_j}} \\ &{v_k} = {u_k} + {b_k} \\ &{y_k} = \varphi \left( {{v_k}} \right) \end{align}\]

Trong đó \({x_1},{x_2},...,{x_m}\) là giá trị của các tín hiệu đầu vào, \({w_{k1}},{w_{k2}},...,{w_{km}}\) là các trọng số tương ứng với các khớp thần kinh liên kết đến nơ-ron có nhãn \(k, {{u_k}}\) là bộ tổ hợp tuyến tính đầu ra (linear combiner output) từ các tín hiệu đầu vào, ${b_k}$ là độ lệch (bias), \(\varphi \left( . \right)\) là hàm kích hoạt (activation function) và ${y_k}$ là tín hiệu đầu ra từ nơ-ron có nhãn $k$.

Các hàm kích hoạt phổ biến

Hàm ngưỡng

Hàm ngưỡng (threshold function) là hàm không liên tục và miền giá trị của hàm chỉ mang hai giá trị là $0$ và $1$. Hàm này được mô tả theo công thức như sau:

\[\begin{align} \varphi \left( v \right) = \left\{ {\begin{array}{*{20}{c}} {1\,\,\,if\,\,v \ge 0}\\ {0\,\,\,if\,\,v < 0} \end{array}} \right. \end{align}\]

Trong kỹ thuật, hàm này còn được gọi là hàm bước Heaviside (Heaviside step function). Tương ứng với hàm kích hoạt này, giá trị đầu ra \({y_{k}}\) của nơ-ron có nhãn $k$ sẽ là:

\[\begin{align} {y_k} = \left\{ {\begin{array}{*{20}{c}} {1\,\,\,if\,\,{v_k} \ge 0}\\ {0\,\,\,if\,\,{v_k} < 0} \end{array}} \right. \end{align}\]

Trong đó:

\[\begin{align} {v_k} = \sum\limits_{j = 1}^m {{w_{kj}}{x_j} + {b_k}} \end{align}\]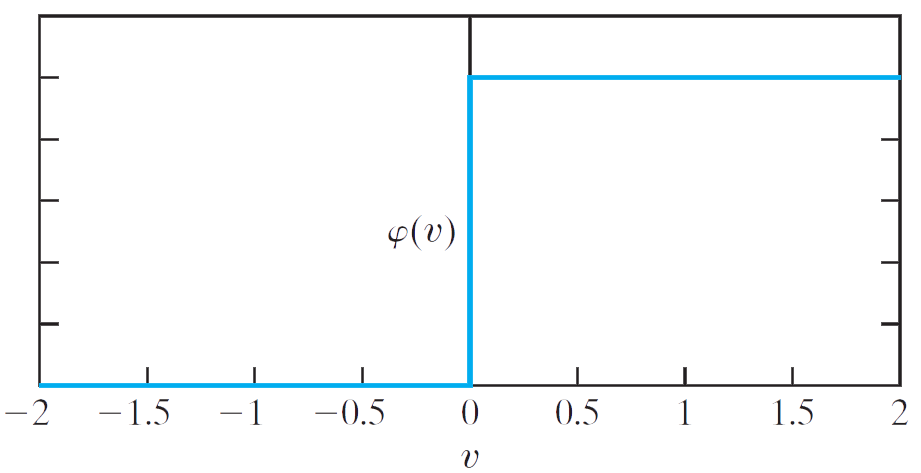

Trong thực tế, hiện nay hàm ngưỡng ít được sử dụng do hàm này không có đạo hàm tại điểm $0$ và đạo hàm tại các điểm còn lại đều bằng $0$, các thuật toán dựa trên gradient đều không phù hợp khi sử dụng hàm ngưỡng làm hàm kích hoạt.

Hàm ReLU

Hàm ReLU (Rectified Linear Unit) được giới thiệu bởi Hahnloser vào năm 2000 và hàm này được định nghĩa như sau: \begin{align} \varphi \left( v \right) = \max \left( {0,v} \right) \end{align}

Định nghĩa trên có thể được viết lại như sau:

\[\begin{align} \varphi \left( v \right) = \left\{ {\begin{array}{*{20}{c}} {0\,\,\,if\,\,v \le 0}\\ {v\,\,\,if\,\,v > 0} \end{array}} \right. \end{align}\]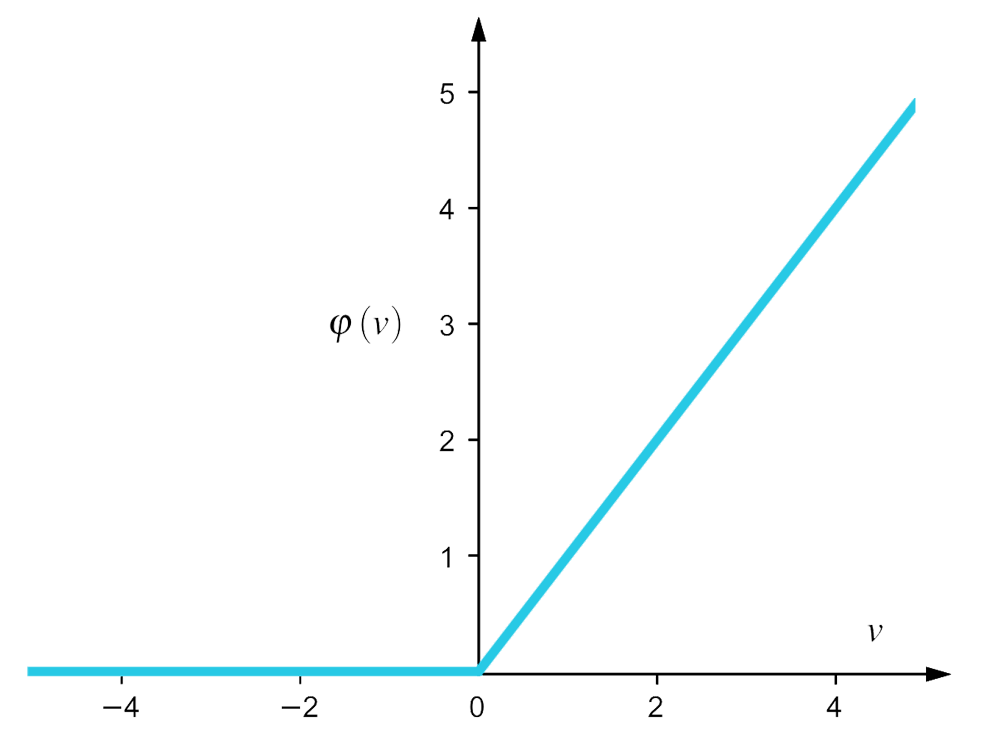

Vào năm 2011, lần đầu tiên người ta đã chứng minh được rằng hàm ReLU giúp cho việc huấn luyện các mạng nơ-ron trở nên tốt hơn so với các hàm kích hoạt khác được sử dụng rộng rãi trước năm 2011. Do đó đây là một hàm được sử dụng làm hàm kích hoạt phổ biến rộng rãi nhất trong các mạng nơ-ron cho đến hiện nay.

Hàm Logistic Sigmoid

Hàm logistic sigmoid có đồ thị là đường cong hình chữ S đặc trưng. Hàm này được định nghĩa như sau:

\[\begin{align} \varphi \left( v \right) = \frac{1}{{1 + {e^{ - v}}}} \end{align}\]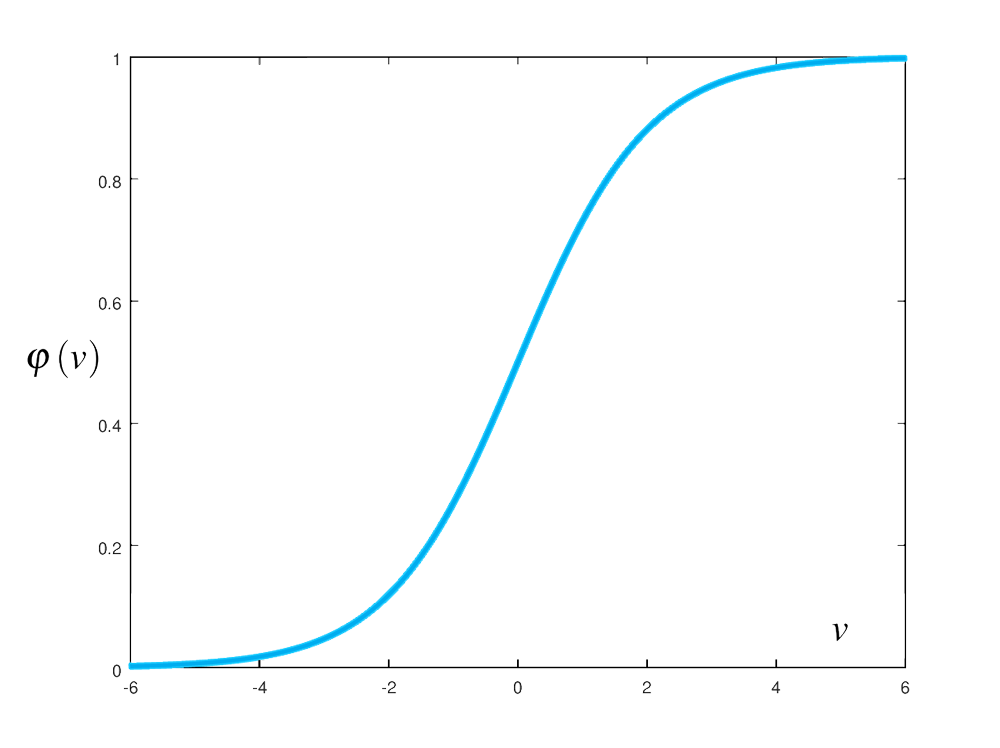

Hàm logistic sigmoid là hàm liên tục, có miền xác định là \(\left( { - \infty , + \infty } \right)\) và có miền giá trị là \(\left( { - 1,1} \right)\). Nhìn vào đồ thị của hàm ở hình trên, chúng ta có thể thấy rằng nếu đầu vào của hàm này càng lớn, giá trị đầu ra sẽ càng tiến gần đến 1. Với đầu vào có giá trị càng âm thì giá trị đầu ra của hàm càng tiến gần đến 0. Trước đây, hàm logistic sigmoid thường được ưu tiên sử dụng làm hàm kích hoạt trong các mạng nơ-ron do tính chất khả vi và có một đạo hàm đẹp có thể được tính toán khá dễ dàng:

\[\begin{align} \frac{{d\varphi \left( v \right)}}{{dv}} = \left( {1 - \varphi \left( v \right)} \right)\varphi \left( v \right) = \varphi \left( v \right)\varphi \left( { - v} \right) \end{align}\]

Hàm Hyperbolic Tangent

Hàm hyperbolic tangent cũng là một hàm liên tục, có miền xác định là $\left( { - \infty , + \infty } \right)$ và có miền giá trị là \(\left( { - 1,1} \right)\).

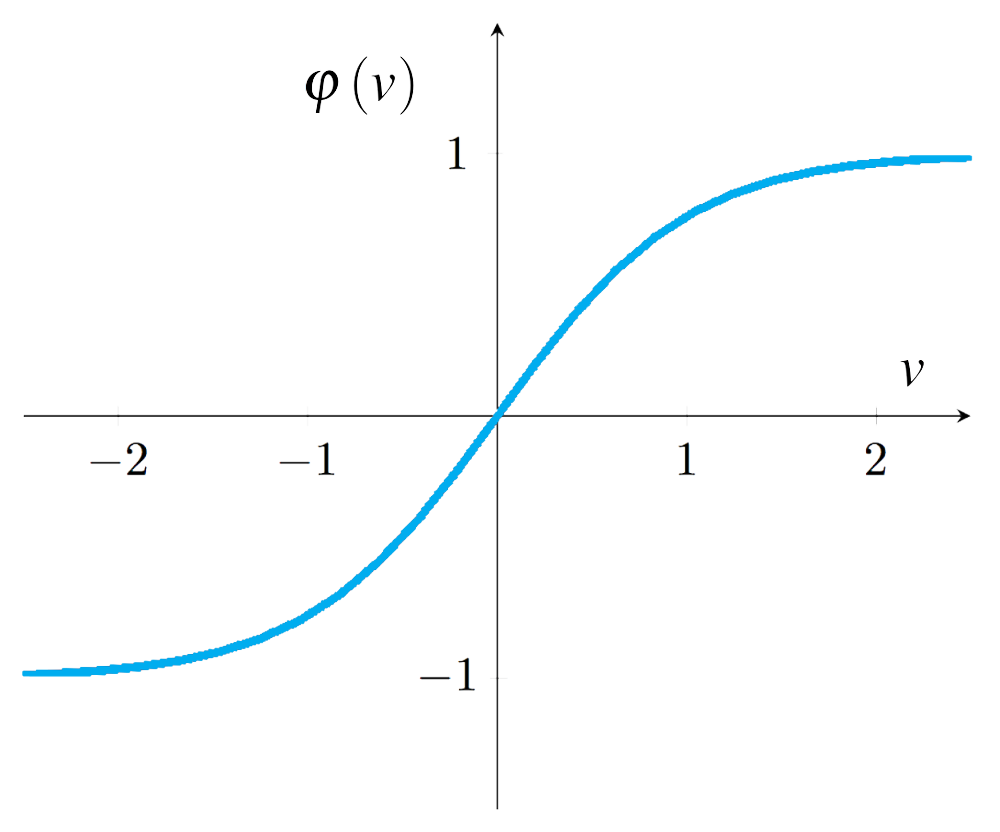
Tương tự như hàm logistic sigmoid, đồ thị của hàm hyperbolic tangent cũng có đồ thị hình chữ S như trong hình trên. Mối liên hệ giữa hàm logistic sigmoid và hàm hyperbolic tangent được biểu diễn qua công thức sau:

\[\begin{align} \tanh \left( v \right) = 2\sigma \left( {2v} \right) - 1 \end{align}\]

Mặc dù hàm logistic sigmoid là một hàm đẹp, nhưng đôi khi cũng gặp một số vấn đề. Nếu đầu vào có giá trị càng âm thì giá trị đầu ra của hàm logistic sigmoid càng gần $0$, điều đó sẽ làm cho quá trình huấn luyện mạng nơ-ron trở nên chậm chạp, các trọng số được cập nhật với sự thay đổi giá trị rất ít. Trong trường hợp này, hàm hyperbolic tangent là một sự lựa chọn thay thế tốt cho hàm logistic sigmoid.

Hàm Softmax

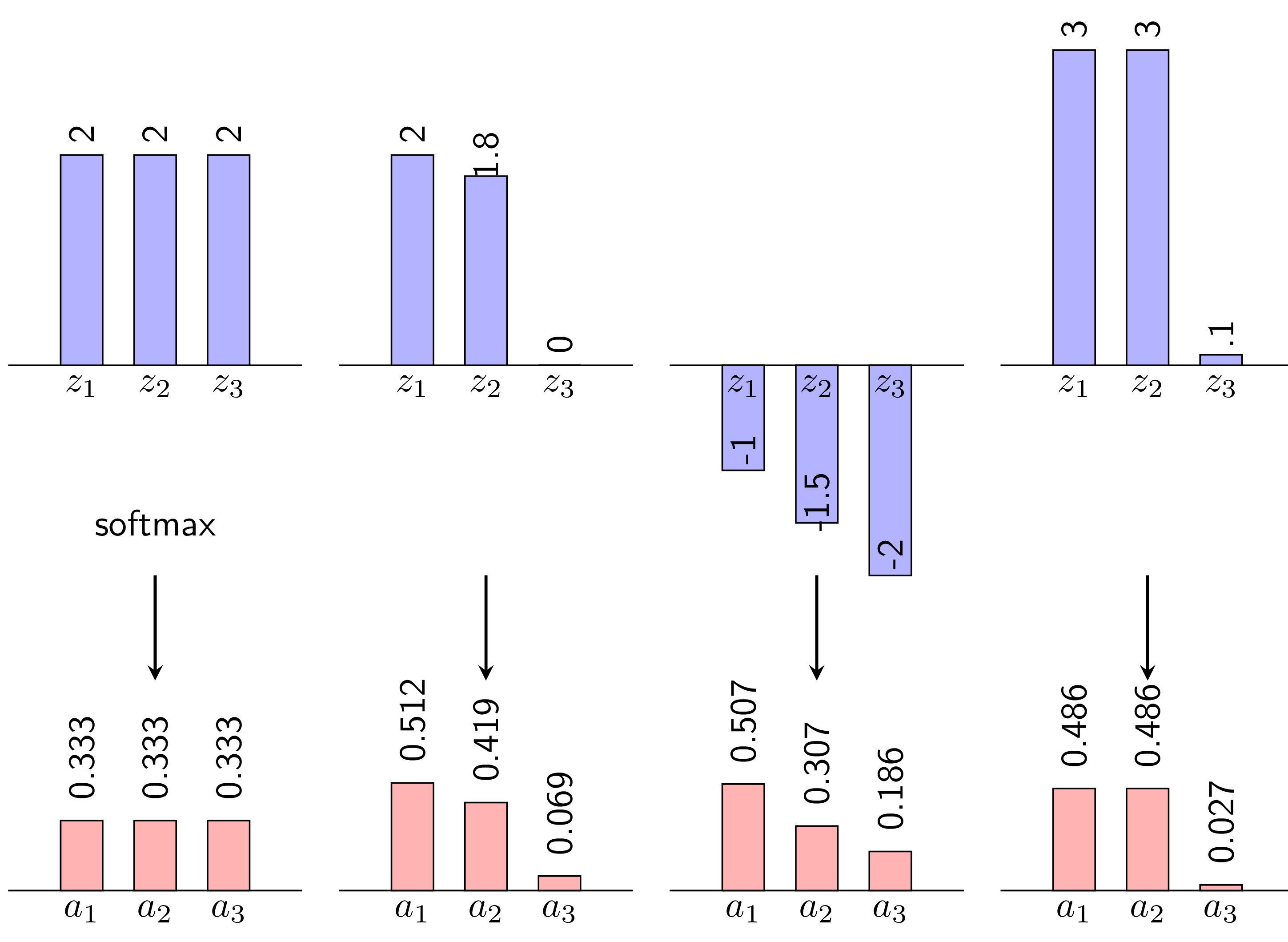
Trong bài toán phân loại nhiều lớp với $K$ lớp cụ thể, hàm softmax được dùng để tính phân bố xác suất của dữ liệu đầu vào trên mỗi lớp cho trước. Hàm softmax sẽ chuyển đổi một vector $K$ chiều chứa các phần tử có giá trị là một số thực bất kỳ $z_{j}$ thành một vector $K$ chiều chứa các phần tử $a_{j}$ có giá trị trong miền \(\left( {0,1} \right)\):

\[\begin{equation} a_{j} = \frac{exp(z_{j})}{\sum^K_{k=1} exp(z_{k})},\quad j = 1, ..., K \end{equation}\]

Mỗi giá trị $a_{j}$ là xác suất mà dữ liệu đầu vào sẽ thuộc vào lớp $j$ tương ứng và tổng của các giá trị này sẽ bằng $1$. Chúng ta phân lớp cho dữ liệu đầu vào bằng cách chọn lớp có giá trị xác suất $a_{j}$ lớn nhất.

Feedforward Neural Network

Mạng nơ-ron được tạo thành khi chúng ta kết nối các nơ-ron đơn lẻ lại với nhau. Trong mạng nơ-ron, các nơ-ron được tổ chức thành từng lớp (layer). Ở dạng đơn giản nhất, mạng nơ-ron chỉ có duy nhất một lớp đầu ra (output layer). Các tín hiệu đầu vào được truyền trực tiếp thông qua các trọng số. Thiết kế đơn giản này tạo nền tảng cho các mạng nơ-ron khác có cấu trúc phức tạp hơn.

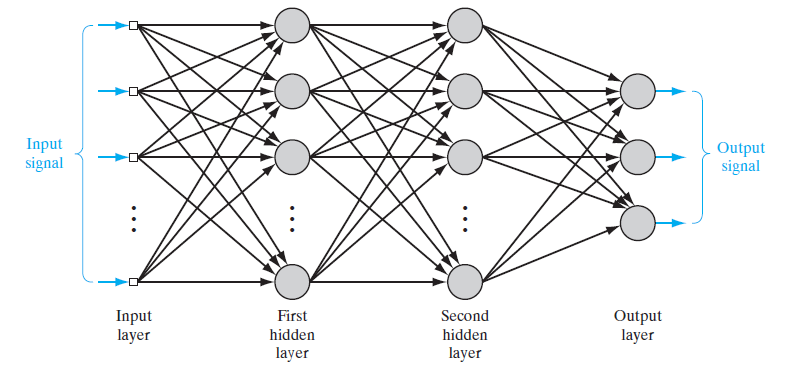
Hình bên dưới dưới đây cho thấy kiến trúc của một mạng nơ-ron truyền thẳng (feedforward neural network) rất giống với kiến trúc được đề xuất bởi McCulloch và Pitt vào năm 1943. Thông thường các nơ-ron được xếp thành các lớp (layer) và kết nối với nhau. Lớp đầu tiên bên trái là lớp đầu vào (input layer) và lớp cuối cùng bên phải là lớp đầu ra (output layer), các lớp còn lại ở giữa là lớp ẩn (hidden layer). Các nơ-ron trong một lớp sẽ có trọng số (weight) tương ứng với kết nối đến nơ-ron của lớp khác. Mỗi một nơ-ron trong bất kỳ lớp nào của mạng đều được kết nối với tất cả các nơ-ron trong lớp đứng trước. Kiểu kết nối này được gọi là kết nối đầy đủ (fully connected). Không có bất kỳ kết nối nào giữa các nơ-ron trong cùng một lớp với nhau. Các tín hiệu chỉ được truyền thẳng theo một chiều từ trái sang phải qua các nơ-ron và không kết nối nào truyền tín hiệu theo chiều ngược lại.