Ý tưởng của mô hình Skip-gram đối lập với CBOW, các từ mục tiêu bây giờ trở thành đầu vào và các từ ngữ cảnh trong câu trở thành đầu ra. Cho từ mục tiêu \({w_c}\) tại vị trí $c$ trong câu văn bản, khi đó đầu vào của mô hình Skip-gram cũng chính là từ mục tiêu \({w_c}\) và đầu ra của mô hình là các từ ngữ cảnh \(\left( {{w_{c - m}},...,{w_{c - 1}},{w_{c + 1}},...{w_{c + m}}} \right)\) xung quanh từ \({w_c}\) trong phạm vi \(m\).

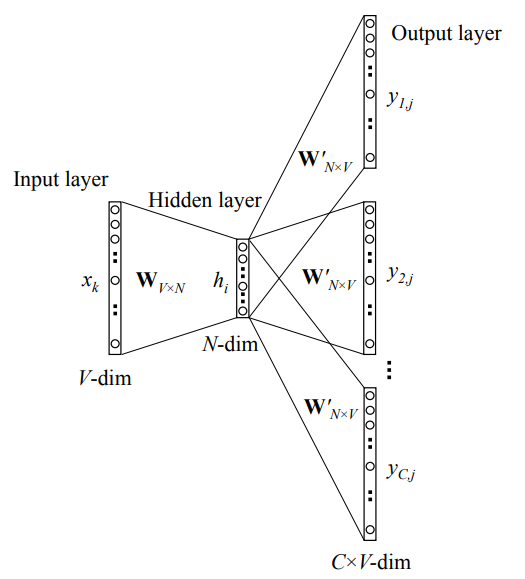
Mô hình Skip-gram tổng quát được thể hiện trong hình bên trên với đầu vào gồm một từ mục tiêu duy nhất, đầu ra gồm $C$ từ ngữ cảnh xung quanh từ mục tiêu đầu vào, $V$ là kích thước của tập từ vựng trong tập ngữ liệu dùng để huấn luyện và hyperparameter $N$ là kích thước của hidden layer. Các unit thuộc các layer kế cận nhau được kết nối theo kiểu fully connected. Gọi \({v_{{w_I}}}\) là vector đầu vào đại diện cho từ đầu vào duy nhất ${w_I}$. Các từ trong câu đầu vào của mô hình được chuyển về dưới dạng vector one-hot ${x^{\left( k \right)}}$:

\[\begin{align} {x^{\left( k \right)}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_k}}\\ \vdots \\ {{x_V}} \end{array}} \right] \end{align}\]

Ma trận $W$ với kích thước $V\times N$ là ma trận trọng số từ lớp đầu vào đến lớp ẩn có dạng như sau:

\[\begin{align} {W_{V \times N}} = \left[ {\begin{array}{*{20}{c}} {{w_{11}}}&{{w_{12}}}& \cdots &{{w_{1N}}}\\ {{w_{21}}}&{{w_{22}}}& \cdots &{{w_{2N}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{w_{{\rm{V1}}}}}&{{w_{{\rm{V2}}}}}& \ldots &{{w_{{{VN}}}}} \end{array}} \right] \end{align}\]

Trong ma trận $W$, mỗi hàng thứ $i$ của ma trận chính là vector đại diện tương ứng cho từ thứ $i$ trong tập từ vựng và $N$ do chúng ta định nghĩa. Ma trận này thu được sau khi huấn luyện là kết quả cần quan tâm do chứa các vector đại diện cho các từ trong tập từ vựng. Ma trận $h$ của lớp ẩn kích thước là $N\times 1$ có dạng như sau:

\[\begin{align} h = \left[ {\begin{array}{*{20}{c}} {{h_1}}\\ {{h_2}}\\ \vdots \\ {{h_N}} \end{array}} \right] \end{align}\]

Mỗi phần tử của ma trận $h$ tương ứng với output của mỗi hidden layer unit. Activation function của các hidden layer unit đều là hàm tuyến tính \(\varphi \left( x \right) = x\). Ma trận $W’$ có chiều $N\times V$ là ma trận trọng số từ lớp ẩn đến lớp đầu ra có dạng như sau:

\[\begin{align} W_{N \times V}^{'} = \left[ {\begin{array}{*{20}{c}} {w_{11}^{'}}&{w_{12}^{'}}& \cdots &{w_{1V}^{'}}\\ {w_{21}^{'}}&{w_{22}^{'}}& \cdots &{w_{2V}^{'}}\\ \vdots & \vdots & \ddots & \vdots \\ {w_{N1}^{'}}&{w_{N2}^{'}}& \cdots &{w_{NV}^{'}} \end{array}} \right] \end{align}\]

Trong đầu ra thay vì chỉ có một phân phối, chúng ta tạo ra $C$ phân phối. Gọi $y_{c, j}$ là phần tử thứ $j$ trong vector đầu ra thứ $c$ với $c = 1, 2,… C$. Do ${x^{\left( k \right)}}$ là vector one-hot đầu vào duy nhất nên $h$ được tính như sau:

\[\begin{equation} h = W_{\left( {k, \cdot } \right)}^T = v{}_{{w_I}}^T \end{equation}\]

Giá trị của $y_{c,j}$ biểu diễn cho xác suất xuất hiện của từ thứ $j$ trong tập từ vựng gồm $V$ từ ở đầu ra thứ $c$ được tính như sau:

\[\begin{equation} p\left( {{w_{c,j}} = {w_{O,c}}|{w_I}} \right) = {y_{c,j}} = \frac{{\exp \left( {{u_{c,j}}} \right)}}{{\sum\limits_{j' = 1}^V {\exp \left( {{u_{j'}}} \right)} }} \end{equation}\]

Trong đó ${w_{c,j}}$ là từ thứ $j$ trong tập từ vựng gồm $V$ từ tương ứng ở đầu ra thứ $c$ và ${w_{O,c}}$ là từ ngữ cảnh đầu ra thứ $c$ hiện tại. Do các đầu ra đều sử dụng chung các trọng số nên $u_{c, j}$ được tính bằng công thức sau:

\[\begin{align} {u_{c,j}} = {u_j} = {v{_{{w_j}}^{'}}^T} \cdot h \text{ với } c = 1,2,...,C \end{align}\]

Trong đó \(v{_{{w_j}}^{'}}\) là vector đầu ra của từ thứ $j$ trong tập từ vựng ${w_j}$ và lấy từ cột tương ứng của ma trận trọng số $W’$. Hàm mất mát $E$ được cho bởi công thức sau:

\[\begin{align} E &= - \log p\left( {{w_{O,1}},{w_{O,2}},...,{w_{O,C}}|{w_I}} \right)\\ &= - \log \prod\limits_{c = 1}^C {\frac{{\exp \left( {{u_{c,j_c^*}}} \right)}}{{\sum\limits_{j' = 1}^V {\exp \left( {{u_{j'}}} \right)} }}}\\ &= - \sum\limits_{c = 1}^C {{u_{j_c^*}}} + C \cdot \log \sum\limits_{j' = 1}^V {\exp \left( {{u_{j'}}} \right)} \end{align}\]

Trong đó $j^{*}_{c}$ là vị trí hiện tại của từ ngữ cảnh thứ $c$ trong tập từ vựng. Các trọng số từ lớp ẩn đến lớp đầu ra trong ma trận $W’$ được cập nhật theo phương trình sau:

\[\begin{align} {v{_{{w_j}}^{'}}^{\left( {new} \right)}} = {v{_{{w_j}}^{'}}^{\left( {old} \right)}} - \eta \cdot E{I_j} \cdot h \text{ với } j = 1,2,...,V \end{align}\]

Trong đó $E{I_j}$ được tính như sau:

\[\begin{align} E{I_j} = \sum\limits_{c = 1}^C {\frac{{\partial E}}{{\partial {u_{c,j}}}}} \end{align}\]

Tiếp đến các trọng số trong ma trận $W$ từ lớp đầu vào đến lớp ẩn được cập nhật như sau:

\[\begin{equation} {v_{{w_I}}}^{\left( {new} \right)} = {v_{{w_I}}}^{\left( {old} \right)} - \eta \cdot E{H^T} \end{equation}\]

Trong đó $EH$ là một vector có $N$ chiều và mỗi phần tử của nó được tính như sau:

\[\begin{align} E{H_i} = \sum\limits_{j = 1}^V {E{I_j} \cdot w_{ij}^{'}} \end{align}\]