Giới thiệu thuật toán Gradient Descent

Thuật toán gradient descent là một thuật toán tối ưu hóa được sử dụng trong các bài toán trí tuệ nhân tạo. Thuật toán này đã được đề xuất từ rất lâu trước khi khoa học máy tính được phát triển. Thuật toán gradient descent được đặt tên theo khái niệm “gradient” (độ dốc của một hàm số) trong toán học. Khi chúng ta muốn tìm giá trị nhỏ nhất của một hàm số, chúng ta cần phải tìm đến độ dốc của hàm số đó và giảm dần độ dốc để đến vị trí cực tiểu của hàm số.

Thuật toán gradient descent được đưa ra vào khoảng giữa thế kỷ 19 bởi nhà toán học Pierre-Simon Laplace. Tuy nhiên thuật toán này chỉ được sử dụng rộng rãi trong thế kỷ 20 sau khi công nghệ tính toán phát triển mạnh mẽ. Trong những năm 1950 và 1960, thuật toán gradient descent được sử dụng khá nhiều trong nghiên cứu thống kê và kỹ thuật điều khiển. Trong những năm 1970, thuật toán này được ứng dụng trong các bài toán tối ưu hóa liên quan đến mô hình hóa dữ liệu. Sau đó với sự phát triển của máy tính và trí tuệ nhân tạo, thuật toán gradient descent đã trở thành một trong những thuật toán tối ưu hóa quan trọng nhất ở lĩnh vực trí tuệ nhân tạo.

Trong toán học, gradient là một trường hợp tổng quát của đạo hàm. Trong khi đạo hàm được định nghĩa trên các hàm số đơn biến và có giá trị vô hướng, gradient có giá trị là một vector. Giống như đạo hàm, gradient biểu diễn độ dốc tiếp tuyến (tangent) của đồ thị hàm số. Gradient của một hàm đa biến \(f\left( {{x_1},..,{x_M}} \right)\) là một vector chứa tất cả các đạo hàm riêng phần (partial derivatives) của hàm \(f\) và được ký hiệu là \(\nabla f\). Phần tử \(i\) trong gradient là đạo hàm riêng phần của hàm \(f\) theo biến \({x_i}\). Cho hàm \(f:{\mathbb{R}^n} \to \mathbb{R}\) là hàm lồi và khả vi, bài toán chúng ta cần giải quyết là tìm \({x^*}\) sao cho:

\[\begin{align} f\left( {{x^*}} \right) = \min f\left( x \right) \end{align}\]

Xem xét bài toán trên, như chúng ta đã biết rằng để tìm cực tiểu của một hàm lồi, ta cần phải tìm điểm dừng của hàm số đó. Trong toán học, điểm dừng (stationary point) của một hàm khả vi là điểm mà mọi phần tử của gradient tại điểm đó đều bằng \(0\). Ý tưởng của phương pháp gradient descent là chúng ta sẽ bắt đầu tại một điểm tùy ý, sau đó di chuyển dọc theo hướng ngược lại của gradient tại điểm đó, tiếp tục lặp lại quá trình này cho đến khi hy vọng có thể hội tụ tại điểm dừng. Hình bên dưới đã minh họa ý tưởng này.

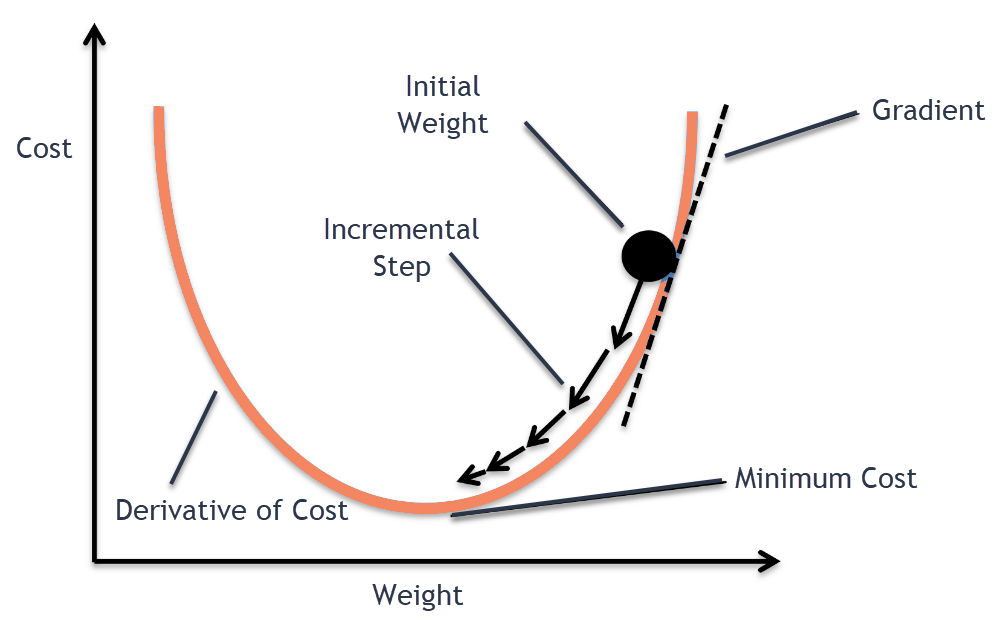
Cụ thể hơn, chúng ta sẽ xác định hướng và kích thước di chuyển thông qua mô tả bằng các công thức toán học. Bắt đầu tại một điểm \({x^{\left( 0 \right)}} \in {\mathbb{R}^n}\) bất kỳ, chúng ta sẽ di chuyển theo hướng \(\nabla f\left( {{x^{\left( k \right)}}} \right)\) tại mỗi lần lặp $k \ge 0$ với kích thước lặp ${t_k}$ (step size) tới điểm tiếp theo \({x^{\left( {k + 1} \right)}}\). Quá trình lặp này được tóm gọn trong công thức sau đây:

\[\begin{align} {x^{\left( {k + 1} \right)}} = {x^{\left( k \right)}} - {t_k}\nabla f\left( {{x^{\left( k \right)}}} \right) \end{align}\]

Chúng ta có thể lựa chọn kích thước lặp cố định ${t_k} = t$ với t là một số dương hoặc kích thước lặp được ước lượng tại mỗi lần lặp thông qua công thức sau:

\[\begin{align} {t_k} = \arg {\min _{t \ge 0}}f\left( {{x^{\left( k \right)}} - t\nabla f\left( {{x^{\left( k \right)}}} \right)} \right) \end{align}\]

Quá trình lặp dừng lại tại một số điểm hoặc khi thỏa mãn điều kiện mà bài toán chúng ta cần giải quyết đặt ra. Với độ chính xác $\varepsilon > 0$ cho trước, thuật toán gradient descent có thể được trình bày cụ thể như sau:

\[\begin{array}{l} 1:\,\,{\rm{Guess}}\,\,{x^{\left( 0 \right)}},\,\,{\rm{set}}\,\,k \leftarrow 0\\ 2:\,\,{\rm{while}}\,\,\left\| {\nabla f\left( {{x^{\left( k \right)}}} \right)} \right\| \ge \varepsilon \,\,{\rm{do}}\\ 3:\,\,\,\,\,\,\,\,\,\,\,\,{x^{\left( {k + 1} \right)}} = {x^{\left( k \right)}} - {t_k}\nabla f\left( {{x^{\left( k \right)}}} \right)\\ 4:\,\,\,\,\,\,\,\,\,\,\,\,k \leftarrow k + 1\\ 5:\,\,{\rm{end}}\,{\rm{while}}\\ 6:\,\,{\rm{return}}\,\,{x^{\left( k \right)}} \end{array}\]

Trong thời gian gần đây, các biến thể của thuật toán gradient descent đã được phát triển để giảm thiểu thời gian tính toán và tăng tốc độ hội tụ của thuật toán. Có nhiều biến thể của thuật toán gradient descent, mỗi biến thể phù hợp với một loại bài toán cụ thể. Dưới đây là một số biến thể phổ biến của thuật toán gradient descent:

• Batch gradient descent: Là biến thể cơ bản nhất của thuật toán gradient descent, nó tính toán đạo hàm trên toàn bộ tập dữ liệu huấn luyện. Tuy nhiên do tính toán trên toàn bộ dữ liệu nên batch gradient descent có thể gặp phải vấn đề về hiệu suất khi tập dữ liệu quá lớn.

• Stochastic gradient descent: Đây là biến thể mà thuật toán chỉ tính toán đạo hàm trên một điểm dữ liệu trong mỗi lần lặp. Do đó, Stochastic gradient descent có thể được sử dụng để giải quyết vấn đề về hiệu suất khi tập dữ liệu quá lớn. Tuy nhiên Stochastic gradient descent có thể dẫn đến độ chính xác không ổn định và tốc độ hội tụ chậm.

• Mini-batch gradient descent: Là biến thể giữa Batch gradient descent và Stochastic gradient descent, nó tính toán đạo hàm trên một tập con của dữ liệu huấn luyện thay vì toàn bộ dữ liệu hoặc một điểm dữ liệu. Mini-batch gradient descent thường được sử dụng để cân bằng giữa độ chính xác và hiệu suất khi làm việc với tập dữ liệu lớn.

• Momentum gradient descent: Biến thể này sử dụng một khái niệm được gọi là momentum để giúp tăng tốc độ hội tụ và tránh được các vùng cục bộ của hàm mất mát. Momentum gradient descent tính toán gradient không chỉ dựa trên gradient hiện tại mà còn dựa trên gradient trước đó để giảm độ nhạy cảm của thuật toán với nhiễu và vùng lõm.

• Nesterov accelerated gradient: Biến thể này cải thiện Momentum gradient descent bằng cách sử dụng công thức truy hồi để tìm kiếm gradient gần với thực tế nhất có thể. Việc này giúp Nesterov accelerated gradient có thể tìm kiếm gradient tốt hơn và giảm độ nhạy cảm của thuật toán với nhiễu.

Ứng dụng thuật toán Gradient Descent trong Machine Learning

Trong machine learning, các mô hình được đào tạo bằng cách điều chỉnh các tham số sao cho chúng có thể dự đoán đầu ra tốt nhất trên tập dữ liệu huấn luyện. Hàm mất mát (loss function) được sử dụng để đo lường mức độ chính xác của mô hình machine learning. Tuy nhiên các hàm mất mát thường là một hàm phi tuyến tính, khó có thể tìm ra giá trị tối thiểu của nó bằng cách tính toán đạo hàm. Do đó chúng ta sử dụng thuật toán gradient descent để tìm giá trị tối thiểu của hàm mất mát.

Các bước chính của thuật toán gradient descent được áp dụng trong machine learning là:

• Định nghĩa hàm mất mát: Đây là hàm số mà chúng ta muốn tối ưu hóa. Lựa chọn hàm mất mát phải phù hợp với bài toán cần giải quyết của machine learning. Hàm mất mát phải là hàm liên tục và khả vi, luôn có giá trị dương, tránh được các điểm tối thiểu cục bộ,… Ví dụ hàm mất mát có thể là tổng bình phương sai số giữa các giá trị dự đoán và giá trị thực tế (Mean Squared Error), hoặc là các hàm phổ biến khác như Cross-entropy loss, Hinge loss, Binary Cross-entropy loss,…
• Khởi tạo các tham số: Các tham số của mô hình machine learning được khởi tạo với những giá trị ngẫu nhiên. Việc khởi tạo giá trị ban đầu cho các tham số của mô hình là rất quan trọng. Khởi tạo không tốt có thể dẫn đến hiện tượng vanishing gradient hoặc exploding gradient, khiến cho việc huấn luyện mô hình trở nên khó khăn và chậm chạp hơn. Một số phương pháp khởi tạo giá trị ngẫu nhiên cho các tham số của mô hình machine learning khi sử dụng thuật toán gradient descent phổ biến bao gồm khởi tạo giá trị ngẫu nhiên với phân phối chuẩn (Gaussian), sử dụng phương pháp khởi tạo số bằng không (zero initialization), sử dụng phương pháp khởi tạo He hoặc Xavier, sử dụng các phương pháp khác như khởi tạo ngẫu nhiên theo phân phối đều (uniform distribution),…
• Tính đạo hàm: Thuật toán sẽ tính toán đạo hàm của hàm mất mát theo các tham số của mô hình. Đạo hàm này sẽ chỉ ra hướng tăng nhanh nhất của hàm mất mát. Các phương pháp tính toán đạo hàm phổ biến nhất cho hàm mất mát có thể là finite difference approximation, symbolic differentiation, automatic differentiation, backpropagation,…
• Cập nhật giá trị tham số: Thuật toán sẽ cập nhật giá trị của tham số trong mô hình theo hướng đối nghịch với đạo hàm của hàm mất mát. Nếu đạo hàm là dương thì chúng ta sẽ giảm giá trị của tham số để giảm thiểu giá trị hiện tại của hàm mất mát. Nó tương ứng với việc dịch chuyển các giá trị của tham số một khoảng nhỏ theo hướng ngược lại của gradient để giảm thiểu giá trị hiện tại của hàm mất mát.
• Lặp lại quá trình: Lặp lại bước 3 và 4 cho đến khi đạt được một điều kiện dừng nhất định hoặc đạt được một số lần lặp tối đa.

Cụ thể hơn về mặt toán học, trong quá trình huấn luyện các mô hình machine learning, thuật toán gradient descent được sử dụng để xác định bộ trọng số $w$ sao cho hàm mất mát \(E\left( w \right)\) đạt cực tiểu. Trong phạm vi của bài viết này, mình chỉ trình bày những ý tưởng tổng quát về quá trình áp dụng thuật toán gradient descent trong machine learning và không đi quá sâu chi tiết.

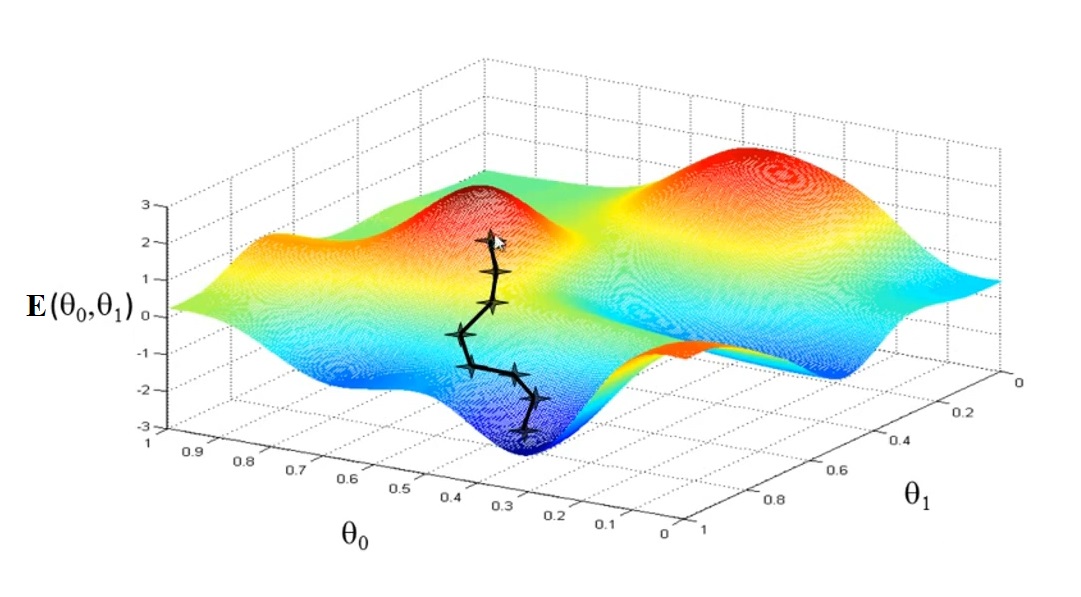
Xét hàm mất mát \(E\left( w \right)\) là một hàm khả vi (differentiable) và liên tục (continuously) với tham số là bộ trọng số $w$. Hàm \(E\left( w \right)\) sẽ ánh xạ bộ trọng số $w$ sang số thực. Chúng ta sẽ tìm \(w^*\) thỏa mãn điều kiện:

\[\begin{align} \nabla E\left( {{w^*}} \right) = 0 \end{align}\]

Trong đó, $\nabla$ là toán tử gradient:

\[\begin{align} \nabla = {\left[ {\frac{\partial }{{\partial {w_1}}},\frac{\partial }{{\partial {w_2}}},...,\frac{\partial }{{\partial {w_M}}}} \right]^T} \end{align}\]

\(\nabla E\left( w \right)\) là gradient của hàm mất mát:

\[\begin{align} \nabla {\rm E}\left( w \right) = {\left[ {\frac{{\partial E}}{{\partial {w_1}}},\frac{{\partial E}}{{\partial {w_2}}},...,\frac{{\partial E}}{{\partial {w_M}}}} \right]^T} \end{align}\]

Chúng ta bắt đầu bằng cách tạo một ước đoán ngẫu nhiên ban đầu là \({w_0}\), sau đó cập nhật các trọng số này sao cho giá trị hàm mất mát \({\rm E}\left( w \right)\) được giảm dần tại mỗi lần lặp của thuật toán:

\[\begin{align} E\left( {{w_{n + 1}}} \right) < E\left( {{w_n}} \right) \end{align}\]

Trong đó \({w_{n}}\) là giá trị cũ của bộ trọng số và \(w_{n + 1}\) là giá trị mới được cập nhật. Thuật toán gradient descent sẽ điều chỉnh bộ trọng số $w$ sao cho hàm mất mát ngày càng đạt giá trị tối thiểu. Việc điều chỉnh bộ trọng số $w$ tại mỗi lần lặp của thuật toán được áp dụng theo hướng ngược lại với vector gradient:

\[\begin{align} {w_{n + 1}} = {w_n} - \eta \nabla E\left( {{w_n}} \right) \end{align}\]

Trong đó $\eta$ là một số thực dương được gọi là learning rate hoặc step size và \(\nabla E\left( {{w_n}} \right)\) là vector gradient tại điểm \(w_{n}\). Giá trị learning rate có ảnh hưởng rất lớn đến việc hội tụ của thuật toán gradient descent. Nếu learning rate nhỏ, thuật toán sẽ hội tụ chậm, nếu learning rate lớn, thuật toán sẽ hội tụ tiến nhanh đến mục tiêu. Tuy nhiên khi learning rate vượt qua một ngưỡng quan trọng nhất định, thuật toán sẽ dẫn đến hiện tượng phân kỳ.